数据结构——并查集

一、认识并查集

并查集，逻辑上是一种集合，能够快速的实现合并和查询，因此得名。这里的查询指的是判断两个元素是否在同一集合。并查集能够高效地管理元素分组情况，为程序设计提供极大的便利。

并查集的本质是树形结构，属于同一集合的元素会位于同一颗树中。由于树的度和深度都不受任何限制，非常自由，我们可以很容易地实现合并查询等基本操作。

二、并查集的基本操作及实现

并查集中的元素除了自己本来带有的属性外，还应有带有两个值来表示其在并查集中的状态：father 这个结点的父节点的索引。

1.初始化

在初始的时候，所有的结点互相之间都没有关系，呈现森林的状态。此时，所有结点都是自己的根结点，所有树的高度都是1（只有一个元素）。

int father[maxn];//父节点的索引

void init(int N)//从1开始初始化N个结点
{
    for(int i = 1;i <= N;i++)
    {
        father[i] = i;
    }
}

2.查询

查询两个元素是否在同一集合中，只需要查询他们的根结点是否相同就可以了。而查找根结点可以通过递归快速地实现：

int find(int x)//查询编号为x的结点的根结点
{
    if(father[x] == x)
        return x;
    else
        return find(father[x]);
}

路径压缩：如果合并的算法不够好的话，并查集可能会出现树的度接近甚至等于树的结点个数的极端情况，也就是退化。如下图，如果后面的结点继续这样连接下去的话，查询的复杂度会变得非常高。

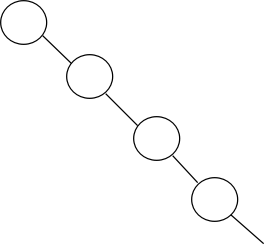
如果一个结点的父结点是谁并不重要的话，我们可以在查询到这个结点的根结点时直接将它连到根结点，这样，下一次查询就只需要一步,可以有效地避免退化。

如图：

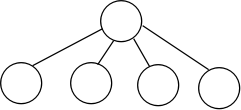
int find(int x)//查询编号为x的结点的根结点
{
    if(father[x] == x)
        return x;
    else
        return father[x] = find(father[x]);//路径压缩
        //return find(father[x]);
}

3.合并

合并两个集合，只需要找出两棵树的根结点，再把其中的某一个连接到另一个就可以了。

void unite(int x, int y)//合并x和y所在的集合
{
    x = find(x);
    y = find(y);
    if(x == y)//如果x和y已在同一集合，那就打扰了
        return;
    father[x] = y;
}