高斯判别分析模型( Gaussian discriminant analysis)及Python实现
1.模型
高斯判别分析模型是一种生成模型,而之前所提到的逻辑回归是一种判别模型,生成模型和判别模型的详细了解可参考这篇文章:
http://blog.sciencenet.cn/home.php?mod=space&uid=248173&do=blog&id=227964
简单的来说,我们的目标都是p(y|x),判别模型是构造一个函数f(x)去逼近p(y|x),而对于生成模型则是通过贝叶斯公式p(y|x) = p(x|y)p(y)/p(x),求得p(x|y)和p(y)来间接得到p(y|x)。
首先,高斯判别分析模型对变量x和y有如下假设:
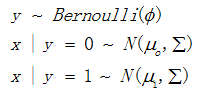
这样,可以给出概率密度函数:

2.评价
该模型的对数似然函数如下:

3.优化
对各个参数进行求导后令等式为0,得到:

Φ是训练样本中结果 y=1 占有的比例。
μ0是 y=0 的样本中特征均值。
μ1是 y=1 的样本中特征均值。
Σ是样本特征方差均值。
4.python代码实现
1 # -*- coding: utf-8 -*- 2 """ 3 Created on Tue Mar 08 16:16:36 2016 4 5 @author: SumaiWong 6 """ 7 8 import numpy as np 9 import pandas as pd 10 from numpy import dot 11 from numpy.linalg import inv 12 13 iris = pd.read_csv('D:iris.csv') 14 dummy = pd.get_dummies(iris['Species']) # 对Species生成哑变量 15 iris = pd.concat([iris, dummy], axis =1 ) 16 iris = iris.iloc[0:100, :] # 截取前一百行样本 17 18 X = iris.ix[:, 0:4] 19 Y = iris['setosa'].reshape(len(iris), 1) #整理出X矩阵 和 Y矩阵 20 21 def GDA(Y, X): 22 theta1 = Y.mean() #类别1的比例 23 theta0 = 1-Y.mean() #类别2的比例 24 mu1 = X[Y==1].mean() #类别1特征的均值向量 25 mu0 = X[Y==0].mean() #类别2特征的均值向量 26 27 X_1 = X[Y==1] 28 X_0 = X[Y==0] 29 A = dot(X_1.T, X_1) - len(Y[Y==1])*dot(mu1.reshape(4,1), mu1.reshape(4,1).T) 30 B = dot(X_0.T, X_0) - len(Y[Y==0])*dot(mu0.reshape(4,1), mu0.reshape(4,1).T) 31 sigma = (A+B)/len(X) #sigma = X'X-n(X.bar)X.bar'=X'[I-1/n 1 1]X
33 return theta1, theta0, mu1, mu0, sigma