巧克力棒(chocolate)
Time Limit:1000ms Memory Limit:64MB
题目描述
LYK 找到了一根巧克力棒,但是这根巧克力棒太长了,LYK 无法一口吞进去。
具体地,这根巧克力棒长为 n,它想将这根巧克力棒折成 n 段长为 1 的巧克力棒,然后
慢慢享用。
它打算每次将一根长为 k 的巧克力棒折成两段长为 a 和 b 的巧克力棒,此时若 a=b,则
LYK 觉得它完成了一件非常困难的事,并会得到 1 点成就感。
LYK 想知道一根长度为 n 的巧克力棒能使它得到最多几点成就感。
输入格式(chocolate.in)
第一行一个数 n。
输出格式(chocolate.out)
一个数表示答案。
输入样例
7
输出样例
4
数据范围
对于 20%的数据 n<=5。
对于 50%的数据 n<=20。
对于 80%的数据 n<=2000。
对于 100%的数据 n<=1000000000。
样例解释
将 7 掰成 3+4, 将 3 掰成 1+2, 将 4 掰成 2+2 获得 1 点成就感, 将剩下的所有 2 掰成 1+1
获得 3 点成就感。总共 4 点成就感。
解析:
可以把问题倒过来考虑,与其折巧克力棒,不如拼巧克力棒。
以样例为例:把7看成7个点,每两个点可以合成一个点,那么7就能合成3个点,再将这3个点合成1个点,那么总共就是4个点。
其他数据同理。
每个数能够合成的点的数量为n/2.
代码:
1 #include <iostream> 2 #include <cstdio> 3 4 using namespace std; 5 long long n,ans; 6 int main() { 7 freopen("chocolate.in","r",stdin); 8 freopen("chocolate.out","w",stdout); 9 scanf("%lld",&n); 10 while(n>=2) { 11 n>>=1; 12 ans+=n; 13 } 14 printf("%lld",ans); 15 return 0; 16 }
LYK 快跑!(run)
Time Limit:5000ms Memory Limit:64MB
题目描述
LYK 陷进了一个迷宫! 这个迷宫是网格图形状的。 LYK 一开始在(1,1)位置, 出口在(n,m)。
而且这个迷宫里有很多怪兽,若第 a 行第 b 列有一个怪兽,且此时 LYK 处于第 c 行 d 列,此
时这个怪兽对它的威胁程度为|a-c|+|b-d|。
LYK 想找到一条路径,使得它能从(1,1)到达(n,m),且在途中对它威胁程度最小的怪兽的
威胁程度尽可能大。
当然若起点或者终点处有怪兽时,无论路径长什么样,威胁程度最小的怪兽始终=0。
输入格式(run.in)
第一行两个数 n,m。
接下来 n 行,每行 m 个数,如果该数为 0,则表示该位置没有怪兽,否则存在怪兽。
数据保证至少存在一个怪兽。
输入格式(run.out)
一个数表示答案。
输入样例
3 4
0 1 1 0
0 0 0 0
1 1 1 0
输出样例
1
数据范围
对于 20%的数据 n=1。
对于 40%的数据 n<=2。
对于 60%的数据 n,m<=10。
对于 80%的数据 n,m<=100。
对于 90%的数据 n,m<=1000。
对于另外 10%的数据 n,m<=1000 且怪兽数量<=100。
题解:
二分答案+bfs。
感觉写不出来就打了40分暴力。。
正解应该是这样的:
首先预处理出每个点到最近的怪物的距离
BFS即可(刚开始把所有的怪物全部进队然后bfs)
然后二分答案求解。
代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 using namespace std; 7 const int maxn=1010; 8 int n,m,tot,a[maxn][maxn],v[maxn][maxn]; 9 int xx[5]={0,1,-1,0,0}, 10 yy[5]={0,0,0,1,-1}; 11 queue<int> x,y; 12 bool flag[maxn][maxn]; 13 void color() 14 { 15 while(!x.empty()) 16 { 17 int fx=x.front(); 18 int fy=y.front(); 19 x.pop();y.pop(); 20 for(int i=1;i<=4;i++) 21 { 22 int tx=fx+xx[i]; 23 int ty=fy+yy[i]; 24 if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&!flag[tx][ty]) 25 { 26 flag[tx][ty]=1; 27 v[tx][ty]=v[fx][fy]+1; 28 x.push(tx); 29 y.push(ty); 30 } 31 } 32 } 33 } 34 bool can(int mid) 35 { 36 for(int i=1;i<=n;i++) 37 for(int j=1;j<=m;j++) 38 flag[i][j]=0; 39 while(!x.empty()) x.pop(); 40 while(!y.empty()) y.pop(); 41 x.push(1);y.push(1); 42 flag[1][1]=1; 43 while(!x.empty()) 44 { 45 int fx=x.front(); 46 int fy=y.front(); 47 x.pop(),y.pop(); 48 for(int i=1;i<=4;i++) 49 { 50 int tx=fx+xx[i],ty=fy+yy[i]; 51 if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&!flag[tx][ty]&&!a[tx][ty]&&v[tx][ty]>=mid) 52 { 53 if(tx==n&&ty==m) 54 return 1; 55 flag[tx][ty]=1; 56 x.push(tx); 57 y.push(ty); 58 } 59 } 60 } 61 return 0; 62 } 63 int main() 64 { 65 freopen("run.in","r",stdin); 66 freopen("run.out","w",stdout); 67 scanf("%d%d",&n,&m); 68 for(int i=1;i<=n;i++) 69 for(int j=1;j<=m;j++) 70 { 71 cin>>a[i][j]; 72 if(a[i][j]==1) 73 { 74 x.push(i);y.push(j); 75 flag[i][j]=1;v[i][j]=0; 76 } 77 } 78 color(); 79 if(a[1][1]==1||a[n][m]==1) 80 { 81 cout<<0; 82 return 0; 83 } 84 int l=0,r=m*n,mid,ans=0; 85 while(l<=r) 86 { 87 mid=(l+r)>>1; 88 if(can(mid)) 89 { 90 ans=mid; 91 l=mid+1; 92 } 93 else r=mid-1; 94 } 95 cout<<ans; 96 return 0; 97 }
仙人掌(cactus)
Time Limit:1000ms Memory Limit:64MB
题目描述
LYK 在冲刺清华集训(THUSC) !于是它开始研究仙人掌,它想来和你一起分享它最近
研究的结果。
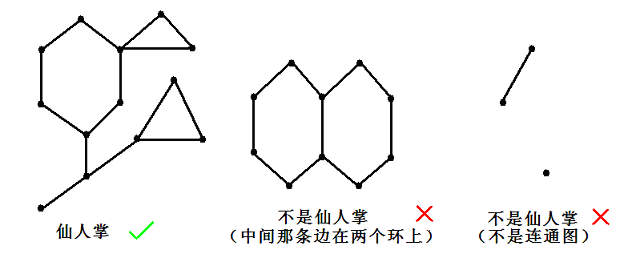
如果在一个无向连通图中任意一条边至多属于一个简单环 (简单环的定义为每个点至多
经过一次) ,且不存在自环,我们称这个图为仙人掌。
LYK 觉得仙人掌还是太简单了,于是它定义了属于自己的仙人掌。
定义一张图为美妙的仙人掌, 当且仅当这张图是一个仙人掌且对于任意两个不同的点 i,j,
存在一条从 i 出发到 j 的路径,且经过的点的个数为|j-i|+1 个。
给定一张 n 个点 m 条边且没有自环的图,LYK 想知道美妙的仙人掌最多有多少条边。
数据保证整张图至少存在一个美妙的仙人掌。
输入格式(cactus.in)
第一行两个数 n,m 表示这张图的点数和边数。
接下来 m 行,每行两个数 u,v 表示存在一条连接 u,v 的无向边。
输出格式(cactus.out)
一个数表示答案
输入样例
4 6
1 2
1 3
1 4
2 3
2 4
3 4
输出样例
4
题解:
第一次提交30分 感觉很不服,然后把<改成了<=,cnt初始值设成1,瞬间到了80分。0.0
还有二十分蜜汁错误。
可能是我离线处理的原因???反正改成在线就对了。0.0
因为数据保证整张图至少存在一个美妙的仙人掌,所以第i个点和第i+1个点一定是连着的。
至少有n-1条边
然后使它尽可能多的方法就是在一条路径上(第i个点到第j个点)不能有两条路径重叠。
以样例为例,选择边 1-2,1-3,2-3,3-4,而不能添加边的原因是:如果再添加一条边(比如1-4),就会有1-3这条边存在于两个简单环中,是不符合要求的,其原因就是1-4和3-4有重叠部分。所以我们让它没有重叠部分的方法就转化成了线段覆盖问题。
代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #define maxn 100005 5 using namespace std; 6 struct Node { 7 int x,y; 8 }node[maxn]; 9 int comp(Node a,Node b) { 10 if(a.y == b.y) return a.x<b.x; 11 return a.y<b.y; 12 } 13 int n,m,Cnt; 14 int main() { 15 freopen("cactus.in","r",stdin); 16 freopen("cactus.out","w",stdout); 17 scanf("%d%d",&n,&m); 18 for(int i=1;i<=m;i++) { 19 int x,y; 20 scanf("%d%d",&x,&y); 21 if(x>y) swap(x,y); 22 if(x+1!=y) node[++Cnt].x=x,node[Cnt].y=y; 23 } 24 sort(node+1,node+1+Cnt,comp); 25 int ans=0,tot=0,e=0; 26 for(int i=1;i<=Cnt;i++) { 27 if(e<=node[i].x) { 28 e=node[i].y; 29 tot++; 30 } 31 } 32 ans=tot+n-1; 33 printf("%d",ans); 34 return 0; 35 }