相关分析
相关分析是研究两个连续变量之间的线性关系
相关性度量
pearson 专门求连续变量之间的相关性
spearman 专门解决离散型变量之间的相关性
proc corr data = double.Fitness pearson spearman; var weight oxygen runtime; 选取分析相关性的变量 run;
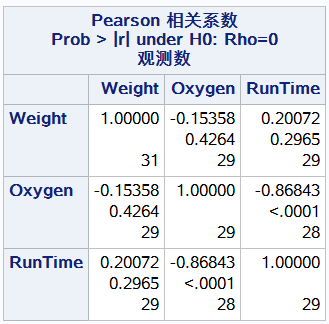
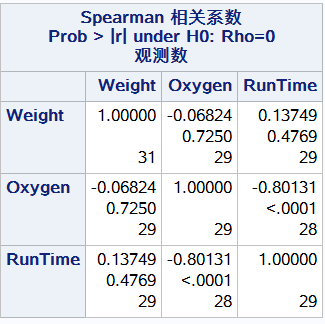
第一个值是weight与weight的相关系数为1 第二个值假设weight与weight不相关情况下所对应的p-value 原假设weight与weight之间无关 p值小拒绝原假设
列联表分析
解决两个离散变量间的相关关系
如果我们只研究两个定型变量之间有无关系,此时可以通过卡方分布检验
如果研究两个变量之间有无因果关系,可以通过趋势检验(r*2 or 2*c)型
- 无序分类资料检验
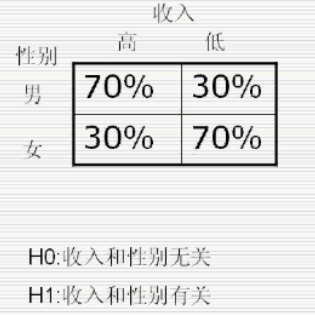
如上图这种属于无序分类资料检测
- 检验统计量在零假设下有(大样本)近似的卡方分布,当该统计量很大或p值很小时,就可以拒绝零假设,从而认为两个变量相关
- 检验的卡方统计量有:pearson卡方统计量和似然比卡方统计量,他们都有渐进的卡方分布
- 相关性度量的指标:Cramer‘s V
- 有序分类资料的检验

- 要对原预测变量进行排序
- 检验统计量在零假设下有(大样本)近似的正态分布。当该统计量很大或p值很小时,就可以拒绝零假设,从而认为这两个变量之间存在有序相关
- 检验的统计量:Mantel-Haenszel
- 相关性度量的指标:spearman系数
无序的分类列子

proc format; value purfmt 1= "$100+" 0 = "<$100"; run; proc freq data = double.b_sales_inc; tables gender*purchase / chisq expected cellchi2 nocol nopercent; format purchase purfmt.; title"性别和购买力之间的关系"; run;
卡方检验关键字:chisq 期望值是根据gender和purchase没有关系情况下,相互独立来计算的

原假设性别与购买力之间没有关系,根据卡方的概率pvalue 拒绝原假设 性别与购买力的关系可以用Cramer V来看 -0.1还是有一定的关系
有序的分类例子
data double.b_sales_inc; set double.b_sales; inclevel = 1*(income = 'Low')+2*(income='Medium')+3*(income = 'High'); run; proc format; value purfmt 1= "$100+" 0="<$100"; run; proc format; value incfmt 1 = "Low income" 2 = "Medium income" 3 = "High income"; run; proc freq data = double.b_sales_inc; table inclevel*purchase /chisq trend measures cl; format inclevel incfmt. purchase purfmt; title "inclevel 和 purchase有序变量的联系"; run;
原假设:在购买力小于100的情况下,收入水平是相等的 通过卡方的概率 推翻原假设 得出收入水平购买力有关
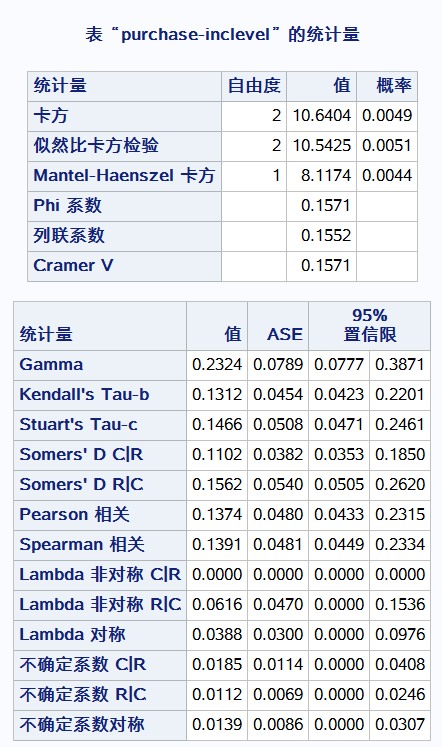
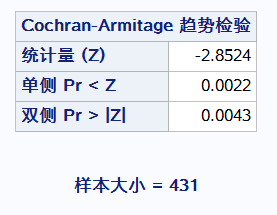
从趋势检验得到统计量z = -2.85可知随着购买力增大,收入水平是越来越高
有没有关系看卡方的概率 越小越相关
然后看统计量Z