词典
跳转表
概念
跳表(skiplist)是一个非常优秀的数据结构,实现简单,插入、删除、查找的复杂度均为O(logN)。LevelDB的核心数据结构是用跳表实现的,redis的sorted set数据结构也是有跳表实现的。跳表同时是平衡树的一种替代的数据结构,但是和红黑树不相同的是,跳表对于树的平衡的实现是基于一种随机化的算法的,这样也就是说跳表的插入和删除的工作是比较简单的。
完整图示
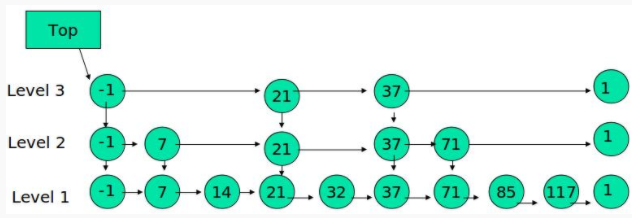
跳表具有如下性质:
(1) 由很多层结构组成
(2) 每一层都是一个有序的链表
(3) 最底层(Level 1)的链表包含所有元素
(4) 如果一个元素出现在 Level i 的链表中,则它在 Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
搜索
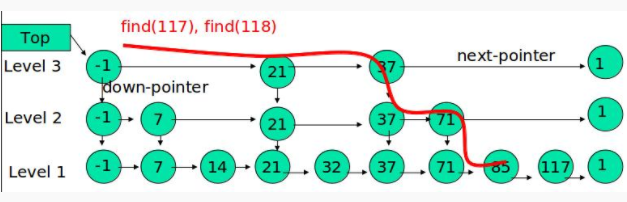
插入

删除
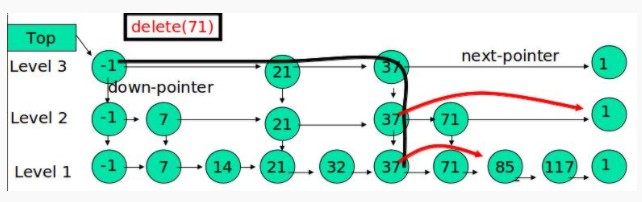
具体如下链接:
https://www.2cto.com/kf/201612/579219.html
c++实现
模板类
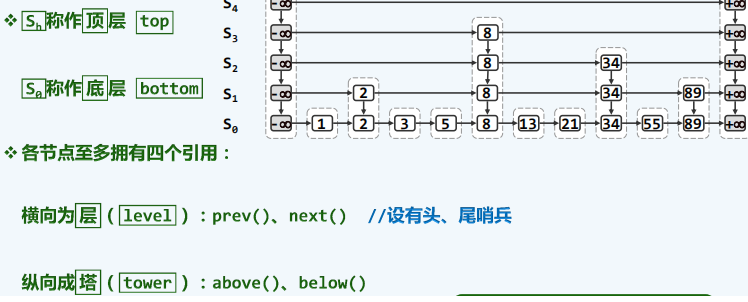



查找算法

插入算法

删除算法

java实现
package com.atguigu.self;
import java.util.*;
/**
* @author wb
*
* 在这里我也从网上查了一些关于跳表的资料,发现了跳表的两种数据结构的设计
* 1. class Node{
* int data; //用于存放数据
* Node next;//用于指向同一层的下一Node
* Node down;//用于指向在数据相同的下一层Node
* }
* 2. class Node{
* int data;
* Node[] forword; //看图可以说明一切,用于指向可以到达的节点
* //随机高度数 k决定节点的高度 h,节点的高度 h决定节点中forword的长度;
* }
*
* 比较上面第一种和第二种数据结构:我选择了第二种,因为我目前觉得
* 例如:新添加一个节点,节点的高度为10,节点数据为2,采用第一种结构,它必定要new 10个Node,然后还得存储相同的数据2,
* 虽然down和next会有不一样,但还是浪费。如果是第二种结构,只需new 一个Node,然后Node中的forward长度设为10,就这样。
* 虽然JVM在创建对象时对对象中的引用和数组是不一样的(next和down是纯粹的引用,而forward是引用数组),但我相信new一次应该比new
* 10次耗时更少吧。
*
*/
public class SkipList {
private class Node{
//存储的数据,当然也可以用泛型
int data;
//leavel层数组
Node[] forword;
public Node() {
}
//int index; //这个变量是专门为了后面的输出好看添加的。
//这个完全没有必要为了好看就去做,因为一旦这样做了,那么在数据跳表中有了相当多的数据节点N时,很不幸(也就
//是在最坏的情况下),如果再添加一个新的元素,而这个元素恰好在header后面的第一个位置,这会导致后面的所有的
//的节点都要去修改一次index域,从而要去遍历整个跳表的最底层。大大的糟糕透顶!
public Node(int data, int leavel){
this.data = data;
this.forword = new Node[leavel];
//this.index = index;
}
public String toString(){
return "[data="+data+", height="+forword.length+"] -->";
}
}
//因为我知道跳表是一个非常优秀的以空间换时间的数据结构设计,
//且其性能在插入、删除甚至要比红黑树高。
//所以我会毫不吝啬的挥霍内存
private static final int DEFAULT_LEAVEL = 3;
//开始标志,(我打算设置其数据项为Integer.MIN_VALUE)
private Node header;
//结束标志,(我打算设置其数据项为Integer.MAX_VALUE)
private Node nil;
//当前节点位置
private Node current;
// 这一变量是为下面的add_tail()方法量身打造的
private Random rd = new Random();
public SkipList(){
//新建header和nil
header = new Node(Integer.MIN_VALUE, DEFAULT_LEAVEL);
nil = new Node(Integer.MAX_VALUE, DEFAULT_LEAVEL);
//这里把它的高度设为1是为了后面的遍历
//把header指向下一个节点,也就是nil
for (int i = DEFAULT_LEAVEL - 1; i >= 0; i --){
header.forword[i] = nil;
}
current = header;
}
/**
* 将指定数组转换成跳表
* @param data
*/
public void addArrayToSkipList(int[] data){
//先将data数组进行排序有两种方法:
//1.用Arrays类的sort方法
//2.自己写一个快速排序算法
quickSort(data);
//System.out.println( Arrays.toString(data));
//
for (int d : data){
//因为数组已经有序
//所以选择尾插法
add_tail(d);
}
}
/**
* 将指定数据添加到跳表
* @param data
*/
public void add(int data){
Node preN = find(data);
if(preN.data != data){
//找到相同的数据的节点不存入跳表
int k = leavel();
Node node = new Node(data, k);
//找新节点node在跳表中的最终位置的后一个位置节点。注意这里的后一个位置节点是指如下:
// node1 --> node2 (node1 就是node2的后一个节点)
dealForAdd(preN, node, preN.forword[0], k);
}
}
/**
* 如果存在 data, 返回 data 所在的节点,
* 否则返回 data 的前驱节点
* @param data
* @return
*/
private Node find(int data){
Node current = header;
int n = current.forword.length - 1;
while(true){
//为什么要while(true)写个死循环呢 ?
while(n >= 0 && current.data < data){
if(current.forword[n].data < data){
current = current.forword[n];
} else if(current.forword[n].data > data){
n -= 1;
} else{
return current.forword[n];
}
}
return current;
}
}
/**
* 删除节点
* @param data
*/
public void delete(int data){
Node del = find(data);
if(del.data == data){
//确定找到的节点不是它的前驱节点
delForDelete(del);
}
}
private void delForDelete(Node node) {
int h = node.forword.length;
for (int i = h - 1; i >= 0; i --){
Node current = header;
while(current.forword[i] != node){
current = current.forword[i];
}
current.forword[i] = node.forword[i];
}
node = null;
}
/**
* 链尾添加
* @param data
*/
public void add_tail(int data) {
Node preN = find(data);
if(preN.data != data){
int k = leavel();
Node node = new Node(data, k);
dealForAdd(current, node, nil, k);
current = node;
}
}
/**
* 添加节点是对链表的相关处理
* @param preNode:待插节点前驱节点
* @param node:待插节点
* @param succNode:待插节点后继节点
* @param k
*/
private void dealForAdd(Node preNode, Node node, Node succNode, int k){
//其实这个方法里的参数 k 有点多余。
int l = header.forword.length;
int h = preNode.forword.length;
if(k <= h){
//如果新添加的节点高度不高于相邻的后一个节点高度
for (int j = k - 1; j >= 0 ; j --){
node.forword[j] = preNode.forword[j];
preNode.forword[j] = node;
}
} else{
//
if(l < k){
//如果header的高度(forward的长度)比 k 小
header.forword = Arrays.copyOf(header.forword, k);
//暂时就这么写吧,更好地处理机制没想到
nil.forword = Arrays.copyOf(nil.forword, k);
for (int i = k - 1; i >= l; i --){
header.forword[i] = node;
node.forword[i] = nil;
}
}
Node tmp;
for (int m = l < k ? l - 1 : k - 1; m >= h; m --){
tmp = header;
while(tmp.forword[m] != null && tmp.forword[m] != succNode){
tmp = tmp.forword[m];
}
node.forword[m] = tmp.forword[m];
tmp.forword[m] = node;
}
for (int n = h - 1; n >= 0; n --){
node.forword[n] = preNode.forword[n];
preNode.forword[n] = node;
}
}
}
/**
* 随机获取高度,(相当于抛硬币连续出现正面的次数)
* @return
*/
private int leavel(){
int k = 1;
while(rd.nextint(2) == 1){
k ++;
}
return k;
}
/**
* 快速排序
* @param data
*/
private void quickSort(int[] data){
quickSortUtil(data, 0, data.length - 1);
}
private void quickSortUtil(int[] data, int start, int end){
if(start < end){
//以第一个元素为分界线
int base = data[start];
int i = start;
int j = end + 1;
//该轮次
while(true){
//从左边开始查找直到找到大于base的索引i
while( i < end && data[++ i] < base);
//从右边开始查找直到找到小于base的索引j
while( j > start && data[-- j] > base);
if(i < j){
swap(data, i, j);
} else{
break;
}
}
//将分界值与 j 互换位置。
swap(data, start, j);
//左递归
quickSortUtil(data, start, j - 1);
//右递归
quickSortUtil(data, j + 1, end);
}
}
private void swap(int[] data, int i, int j){
int t = data[i];
data[i] = data[j];
data[j] = t;
}
//遍历跳表 限第一层
public Map<Integer,List<Node>> lookUp(){
Map<Integer, List<Node>> map = new HashMap<Integer,List<Node>>();
List<Node> nodes;
for (int i = 0; i < header.forword.length; i++){
nodes = new ArrayList<Node>();
for (Node current = header; current != null; current = current.forword[i]){
nodes.add(current);
}
map.put(i, nodes);
}
return map;
}
public void show(Map<Integer,List<Node>> map){
for (int i = map.size() - 1; i >= 0; i --){
List<Node> list = map.get(i);
StringBuffer sb = new StringBuffer("第"+i+"层:");
for (Iterator<Node> it = list.iterator(); it.hasNext();){
sb.append(it.next().toString());
}
System.out.println(sb.substring(0,sb.toString().lastIndexOf("-->")));
}
}
public static void main(String[] args) {
SkipList list = new SkipList();
int[] data = {4, 8, 16, 10, 14};
list.addArrayToSkipList(data);
list.add(12);
list.add(12);
list.add(18);
list.show(list.lookUp());
System.out.println("在本次跳表中查找15的节点或前驱节点为:" + list.find(15));
System.out.println("在本次跳表中查找12的节点或前驱节点为:" + list.find(12) + "n");
list.delete(12);
System.out.println("删除节点值为12后的跳表为:");
list.show(list.lookUp());
}
}
散列表
概念
为什么要散列表
散列方案即事先在词条与 桶地址之间约定的某种映射关系,可描述为从关键码空间到桶数组地址空间的函数
-
例子
以学籍库为例。若某高校2011级共计4000名学生的学号为2011-0000至2011-3999,则可 直接使用一个长度为4000的散列表A[0~3999],并取 hash(key) = key - 20110000 从而将学号为x的学生学籍词条存放于桶单元A[hash(x)]。
实际情况:
尽管词典中实际需要保存的词条 数N(比如25000门远远少于可能出现的词条数R(10^8门,但R个词条中的任何一个都有可能出现在词典中。 -
作用
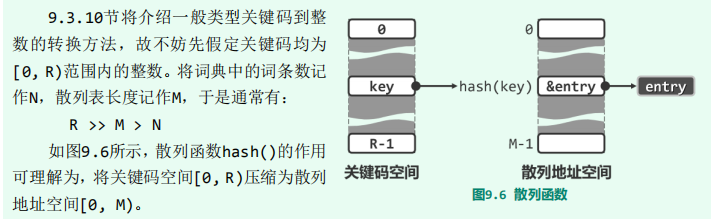
-
设计原则

处理方法
-
除余法
采用除余法时必须将M作素数,否则关键码被映射至[0, M)范围内的均匀度将大 幅降低,发生冲突的概率将随M所含素因子的增多而迅速加大。
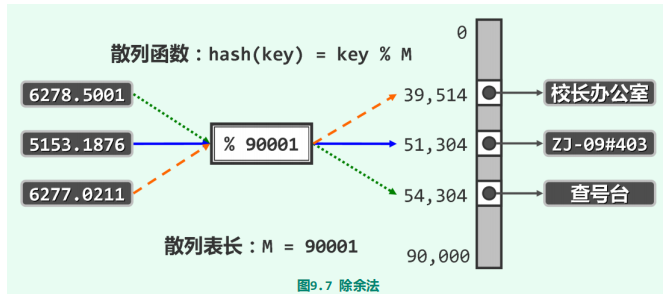
-
MAD法

例如,在如图9.9(a)所示,将关键码: { 2011, 2012, 2013, 2014, 2015, 2016 }
插入长度为M = 17的空散列表后,这组词条将存放至地址连续的6个桶中。尽管这里没任 何关键码的冲突,却具就“更高阶”的均匀性。 为弥补这一不足,可采用所谓的MAD法将关键码key映射,结果如图b
-
伪随机数法
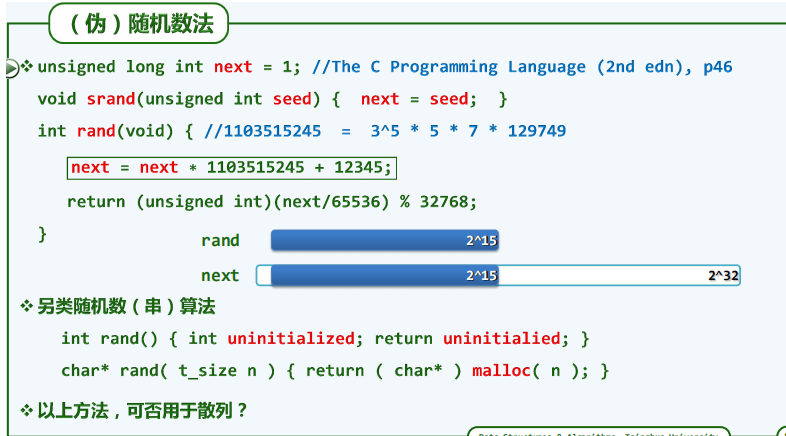
-
多项式法

消除冲突
- 多槽位法
将彼此冲突的每一组词条组织为一个小规模的子词典,分别存放 于它们共同对应的桶单元中。比如一种简便的方法是,统一将各桶细分为更小的称作槽位的若干单元,每一组槽位可组织为向量或列表

如图9.10所示,将各桶细分为四个槽位。 只要相互冲突的各组关键码不超过4个,即可分别保存于对应桶单元内的不同槽位。
-
独立链表法
采用列表(而非向量来实现各子词典,仍以图9.8(a)中的冲突为例,可如图9.11所示令各桶内相互冲突的词条串接成一个列表

-
公共溢出法
在原散列表(图(a)之外另设一个词典结构Doverflow(图(b),一旦在插入词条时发生冲突就将该词条转存至Doverflow中

-
闭散列法
仅仅依靠基本的散列表结构,且就地排解冲突。因为散列地址空间对所有词条开放,故这一新的策略亦称作开放定址;同时,因可用的散列地址 仅限于散列表所覆盖的范围之内,故亦称作闭散列。并提供各种查找方案
-
线性试探
被试探的桶单元在物理空间上依次连贯,会加剧关键码的聚集趋势

-
平方试探
顺着查找链,试探位置的间距将以线性速度增长。于是, 一旦发生冲突,即可“聪明地”尽快“跳离”关键码聚集的区段。只要散列表长度M为素数且装填因50%,则平方试探迟早必将终止于某个空桶,但空间利用率不高

-
双向平方试探

-
懒惰删除
为每个桶另设一个标志位,指示该桶尽管目前为空,但此前确曾存放过词条。