POJ_2653_Pick-up sticks_判断线段相交
Description
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input.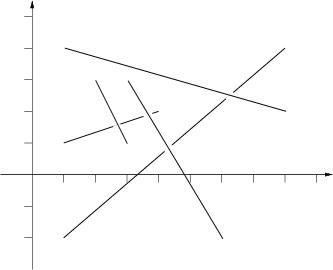
The picture to the right below illustrates the first case from input.

Sample Input
5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0
Sample Output
Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.
斯坦有各种长度的n条。他在地板上随意地扔了一个。在完成投掷后,斯坦试图找到最上面的棍子,那就是这些棍子,这样就没有棍子在上面了。
斯坦注意到,最后一根投掷棒总是在上面,但他想知道上面所有的棍子。斯坦棒非常非常薄,以至于它们的厚度可以被忽略。
暴力可过的一道题。直接枚举所有的所有的线段判断能不能被后面的覆盖即可。
然后判断线段相交用四次叉积判断即可。
代码:
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;
typedef double f2;
#define N 100050
#define eps 1e-6
bool vis[N];
int ans[N],n;
struct Point {
f2 x,y;
Point() {}
Point(f2 x_,f2 y_) :
x(x_),y(y_) {}
Point operator + (const Point &p) const {return Point(x+p.x,y+p.y);}
Point operator - (const Point &p) const {return Point(x-p.x,y-p.y);}
Point operator * (f2 rate) const {return Point(x*rate,y*rate);}
};
f2 dot(const Point &p1,const Point &p2) {return p1.x*p2.x+p1.y*p2.y;}
f2 cross(const Point &p1,const Point &p2) {return p1.x*p2.y-p1.y*p2.x;}
f2 FABS(f2 x) {return x>0?x:-x;}
struct Line {
Point p,v;
Line() {}
Line(const Point &p_,const Point &v_) :
p(p_),v(v_) {}
};
Line a[N];
f2 turn(const Point &p1,const Point &p2,const Point &p3) {
return cross(p3-p1,p2-p1);
}
bool judge(const Line &l1,const Line &l2) {
if(turn(l1.p,l1.v,l2.p)*turn(l1.p,l1.v,l2.v)>0) return 0;
if(turn(l2.p,l2.v,l1.p)*turn(l2.p,l2.v,l1.v)>0) return 0;
return 1;
}
void init() {
memset(vis,0,sizeof(vis)); ans[0]=0;
}
void solve() {
init();
int i,j;
f2 x,y,z,w;
int fir=0;
for(i=1;i<=n;i++) {
scanf("%lf%lf%lf%lf",&a[i].p.x,&a[i].p.y,&a[i].v.x,&a[i].v.y);
}
printf("Top sticks:");
for(i=1;i<=n;i++) {
int flg=0;
for(j=i+1;j<=n;j++) {
if(judge(a[i],a[j])) {
flg=1; break;
}
}
if(!flg) {
if(!fir) {
fir=1;
}else printf(",");
printf(" %d",i);
}
}
puts(".");
}
int main() {
while(scanf("%d",&n)&&n) {
solve();
}
}