BZOJ_1864_[Zjoi2006]三色二叉树_树形DP
题意:
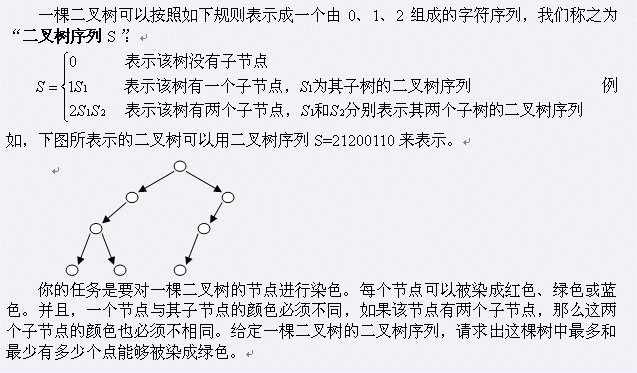
分析:递归建树,然后DP,从子节点转移。
注意到红色和蓝色没有区别,因为我们可以将红蓝互换而方案是相同的。这样的话我们只需要知道当前节点是否为绿色即可。
代码:
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
#define N 500050
int lson[N],rson[N],cnt,n;
int f[N][2],g[N][2],h[N][2];
void build(int x)
{
char s=getchar();
if(s=='0')return ;
lson[x]=++cnt;build(lson[x]);
if(s=='2')
{
rson[x]=++cnt;build(rson[x]);
}
}
void dfs(int x)
{
int u=lson[x],v=rson[x];
if(u==0&&v==0)
{
f[x][0]=f[x][1]=1;
return ;
}
dfs(u);
if(v)
{
dfs(v);
f[x][0]=max(g[u][0]+h[v][0],g[v][0]+h[u][0])+1;
g[x][0]=max(f[u][0]+h[v][0],f[v][0]+h[u][0]);
h[x][0]=max(f[u][0]+g[v][0],f[v][0]+g[u][0]);
f[x][1]=min(g[u][1]+h[v][1],g[v][1]+h[u][1])+1;
g[x][1]=min(f[u][1]+h[v][1],f[v][1]+h[u][1]);
h[x][1]=min(f[u][1]+g[v][1],f[v][1]+g[u][1]);
}
else
{
f[x][0]=max(g[u][0],h[u][0])+1;
h[x][0]=max(f[u][0],g[u][0]);
g[x][0]=max(f[u][0],h[u][0]);
f[x][1]=min(g[u][1],h[u][1])+1;
h[x][1]=min(f[u][1],g[u][1]);
g[x][1]=min(f[u][1],h[u][1]);
}
}
int main()
{
cnt=1;
build(1);
dfs(1);
printf("%d %d",max(max(f[1][0],g[1][0]),h[1][0]),min(min(f[1][1],g[1][1]),h[1][1]));
}