题意:FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a
,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。
n组询问,(1<=n<= 50000)(1<=d<=a,b<=50000)
分析:
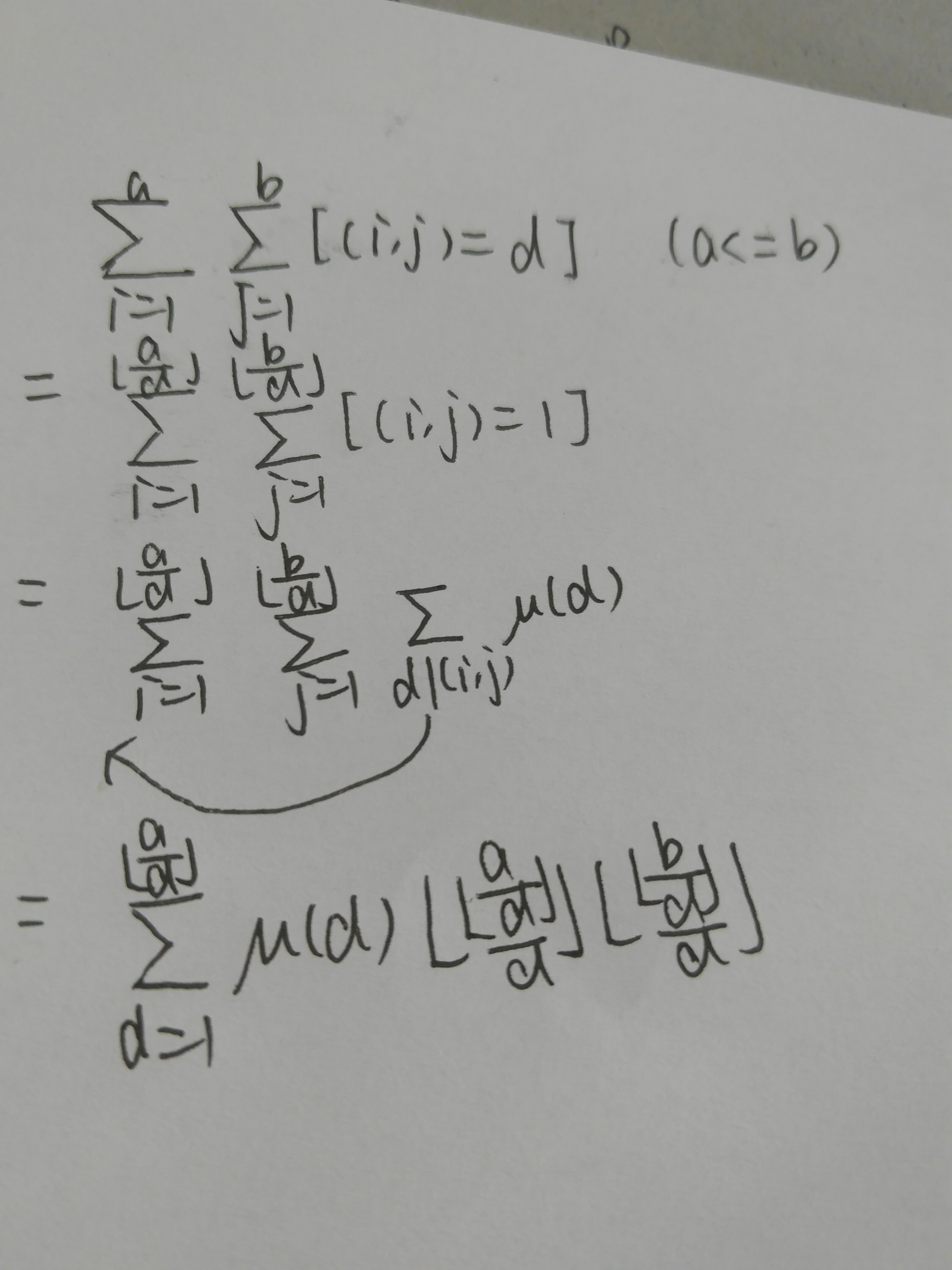
通过处理μ的前缀和把每段$a/i$的值相等的部分一起算。$n/(n/i)$找到值相等的一段的段末位置。
我当时为什么要用图片上传啊。。算了留着吧。
不行还是得补上:
$sumlimits_{i=1}^{n}sumlimits_{j=1}^{m}[gcd(i,j)=d]$
$=sumlimits_{i=1}^{lfloor frac{n}{d}
floor}sumlimits_{j=1}^{lfloorfrac{m}{d}
floor}[gcd(i,j)=1]$
$=sumlimits_{i=1}^{lfloor frac{n}{d}
floor}sumlimits_{j=1}^{lfloorfrac{m}{d}
floor}
sumlimits_{p|(gcd(i,j)}mu(p)$
$=
sumlimits_{p=1}^{lfloor frac{min(n,m)}{d}
floor}mu(p)sumlimits_{i=1}^{lfloor frac{n}{dp}
floor}sumlimits_{j=1}^{lfloorfrac{m}{dp}
floor}$
$=
sumlimits_{p=1}^{lfloor frac{min(n,m)}{d}
floor}mu(p)s(lfloor frac{n}{dp}
floor)s(lfloor frac{m}{dp}
floor)$
代码:
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
#define LL long long
int T,a,b,d;
int miu[50050],prime[50050],vis[50050],cnt,msum[50050];
inline void init()
{
miu[1]=1;
msum[1]=1;
for(int i=2;i<=50000;i++)
{
if(!vis[i])
{
prime[++cnt]=i;
miu[i]=-1;
}
for(int j=1;j<=cnt&&i*prime[j]<=50000;j++)
{
vis[i*prime[j]]=1;
if(i%prime[j]==0)
{
miu[i*prime[j]]=0;
break;
}
miu[i*prime[j]]=-miu[i];
}
msum[i]=msum[i-1]+miu[i];
}
}
int main()
{
init();
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d",&a,&b,&d);
a=a/d;b=b/d;
if(a>b)swap(a,b);
int lst;
LL ans=0;
for(int i=1;i<=a;i=lst+1)
{
lst=min(a/(a/i),b/(b/i));
ans+=1ll*(msum[lst]-msum[i-1])*(a/i)*(b/i);
}
printf("%lld
",ans);
}
}