Divide Two Integers

零. 例行废话

  这个问题其实很早了，也没什么特别tricky的地方，但是我今天突然做到这道题，发现竟然博客上竟然没有比较靠谱的解法，要么大家就是用笨重的累减法，要么就是不要face的公然用除法。关于溢出处理，我发现基本上都没有遵循题目中说的$[ - {2^{31}},{2^{31}} - 1]$的约定，用了long或者long long，实在是太bitch了，有必要由我给大家提供一种比较靠谱的方法。

一. 问题重述

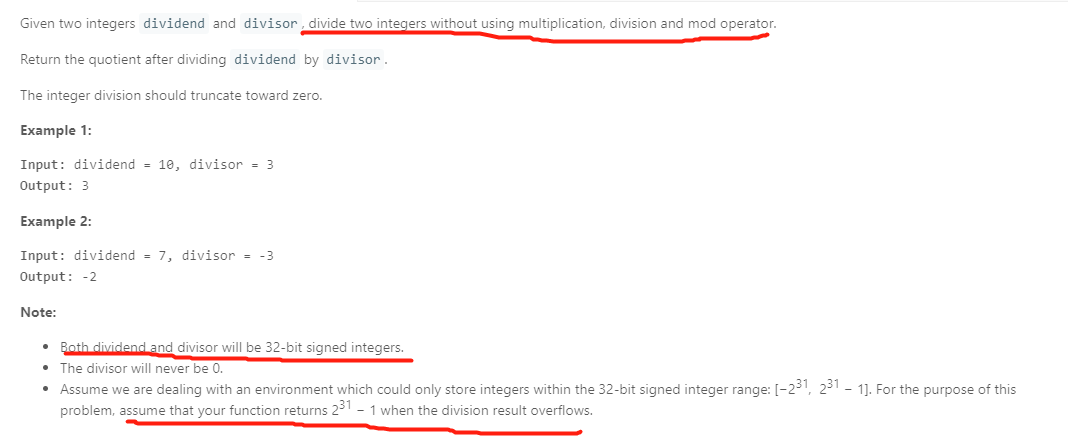
大家先读题，圈重点，显然这个题有两个重要的地方：

1. 不用乘除模实现除法

2. 只能使用32-bit int，也就是要避免溢出

二. bitch的做法

我在提交的时候，随便打开几个答案，发现大家要么是在溢出上做手脚，像这样：

要么是更加猖狂的公然用除法：

三. 正经人的做法

　　其实仔细考虑这个问题，并不是很复杂，主要要解决两个方面的问题，最重要的要找到一种除法的替代方法，一个比较直观的做法是把除法转化为减法，但是我们考虑到这样子做效率太低，交上去怕是要被time out

　　考虑一种高效的，有一定乘法效应的移位算法，我们可以通过不断用移位操作去逼近被除数，然后对余数再进行指数逼近，这样做就很高效了。

        对于溢出，我觉得可以从两个方面来考虑：

• 　　将所有的操作数都转化为负数，因为负数范围大
• 　　在移位的时候及时与-2^30进行比较，以免下次移位溢

四. 源码

using namespace std;

class Solution {
public:
    int divide_(int dividend, int divisor) {
        int divisor_copy = divisor;
        int k = 0;
        while(true){
            int number = (divisor_copy << k);
            if(number >= dividend){
                k ++;
                if(number < (-2 << 29)){
                    break;
                }
            }else{
                break;
            }
        }
       // cout << k << endl;
        if(k == 0){
            return 0;
        }
        if(k == 1){
            return -1 + divide_(dividend - divisor , divisor);
        }
        return (-2 << (k - 2)) + divide_(dividend - (divisor << (k - 1)), divisor);
    }
    int divide(int dividend, int divisor){
        bool flag = true;
        bool f1 = true, f2 = true;
        if(dividend > 0){
            f1 = false;
            dividend = - dividend;
        }
        if(divisor > 0){
            f2 = false;
            divisor = - divisor;
        }
        if(f1 != f2)
            flag = false;
        int result = divide_(dividend, divisor);
        if(flag){
            if(result == (-2 << 30)){
                return -(result + 1);
            }else{
                return -result;
            }
        }
        else
            return result;
    }
};

五. 一个奇怪的事情

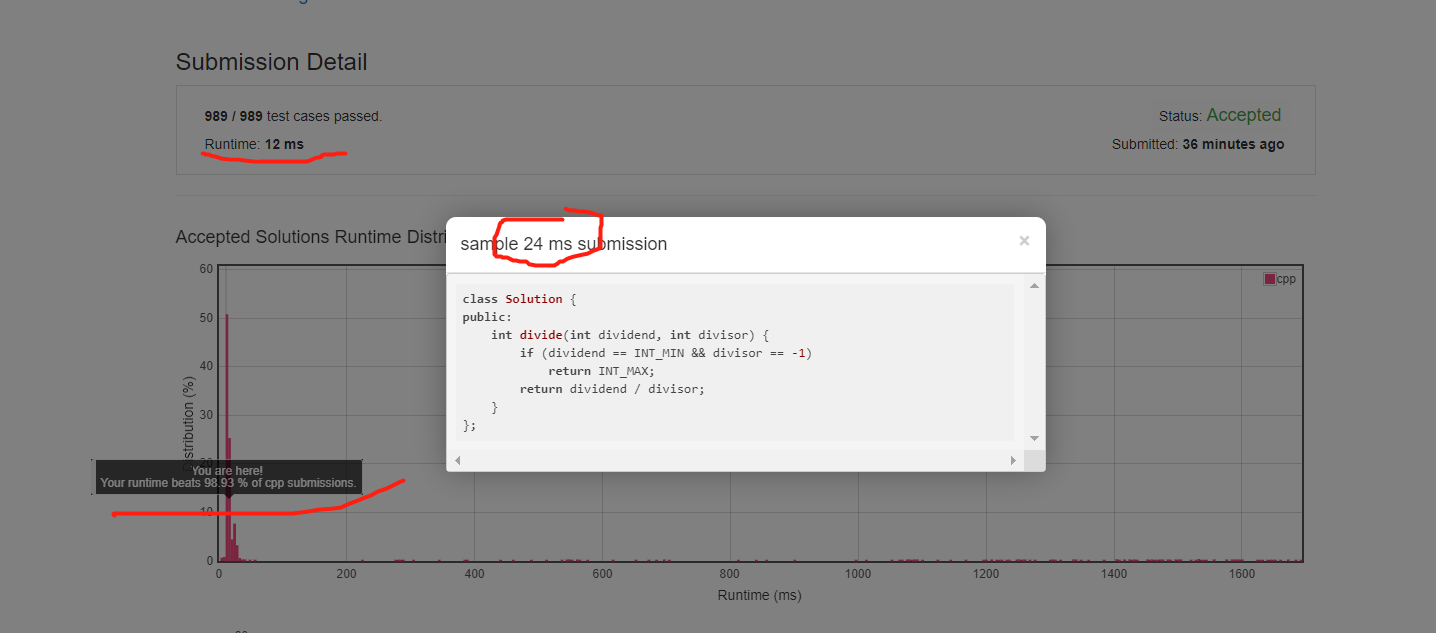
　　我发现一个最最最奇怪的事情是我的很长很长的代码竟然比直接使用除法的快了一倍，难道说我的代码已经突破底层的计算效率了么（伪），见下图：