1. 勾股数
什么是勾股数(毕达哥拉斯三元数)呢?我们得回到从前。在一堂激动人心的数学课上,你了解到,古希腊数学家毕达哥拉斯发现了
某些三元数 (a, b, c) 满足公式 a * a + b * b = c * c ,其中 a 、 b 、 c 都是整数。例如,(3, 4, 5)就是一组有效的勾股数,因
为3 * 3 + 4 * 4 = 5 * 5 或9 + 16 = 25。这样的三元数有无限组。例如,(5, 12, 13)、(6, 8, 10)和(7, 24, 25)都是有效的勾股数。
勾股数很有用,因为它们描述的正好是直角三角形的三条边长,如图所示。
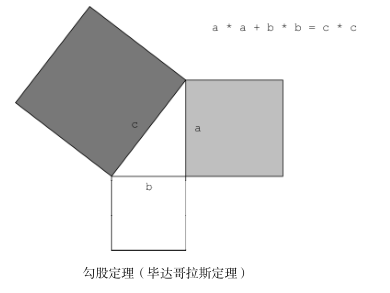
2. 表示三元数
那么,怎么入手呢?第一步是定义一个三元数。虽然更恰当的做法是定义一个新的类来表示三元数,但这里你可以使用具有三
个元素的 int 数组,比如 new int[]{3, 4, 5} ,来表示勾股数(3, 4, 5)。现在你就可以用数组索引访问每个元素了。
3. 筛选成立的组合
假定有人为你提供了三元数中的前两个数字: a 和 b 。怎么知道它是否能形成一组勾股数呢?你需要测试 a * a + b * b 的平方
根是不是整数,也就是说它没有小数部分——在Java里可以使用 expr % 1 表示。如果它不是整数,那就是说 c 不是整数。你可以
用 filter 操作表达这个要求(你稍后会了解到如何将其连接起来成为有效代码):
filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)
假设周围的代码给 a 提供了一个值,并且 stream 提供了 b 可能出现的值, filter 将只选出那些可以与 a 组成勾股数的 b 。你
可能在想 Math.sqrt(a * a + b * b) % 1 == 0 这一行是怎么回事。简单来说,这是一种测试 Math.sqrt(a * a + b * b) 返回的结果是不
是整数的方法。如果平方根的结果带了小数,如9.1,这个条件就不成立(9.0是可以的)。
4. 生成三元组
在筛选之后,你知道 a 和 b 能够组成一个正确的组合。现在需要创建一个三元组。你可以使用map 操作,像下面这样把每个元
素转换成一个勾股数组:
stream.filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)
.map(b -> new int[]{a, b, (int) Math.sqrt(a * a + b * b)});
5. 生成 b 值
胜利在望!现在你需要生成 b 的值。前面已经看到, Stream.rangeClosed 让你可以在给定区间内生成一个数值流。你可以用它
来给 b 提供数值,这里是1到100:
IntStream.rangeClosed(1, 100)
.filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)
.boxed()
.map(b -> new int[]{a, b, (int) Math.sqrt(a * a + b * b)});
请注意,你在 filter 之后调用 boxed ,从 rangeClosed 返回的 IntStream 生成一个Stream<Integer> 。这是因为你的 map会为流中
的每个元素返回一个 int 数组。而 IntStream中的 map 方法只能为流中的每个元素返回另一个 int ,这可不是你想要的!你可以用
IntStream的 mapToObj 方法改写它,这个方法会返回一个对象值流:
IntStream.rangeClosed(1, 100)
.filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)
.mapToObj(b -> new int[]{a, b, (int) Math.sqrt(a * a + b * b)});
6. 生成值
这里有一个关键的假设:给出了 a 的值。 现在,只要已知 a 的值,你就有了一个可以生成勾股数的流。如何解决这个问题呢?
就像 b 一样,你需要为 a 生成数值!最终的解决方案如下所示:
Stream<int[]> pythagoreanTriples =
IntStream.rangeClosed(1, 100).boxed().flatMap(a -> IntStream.rangeClosed(a, 100).filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)
.mapToObj(b -> new int[]{a, b, (int)Math.sqrt(a * a + b * b)}));
好的, flatMap 又是怎么回事呢?首先,创建一个从1到100的数值范围来生成 a 的值。对每个给定的 a 值,创建一个三元数流。
要是把 a 的值映射到三元数流的话,就会得到一个由流构成的流。 flatMap 方法在做映射的同时,还会把所有生成的三元数流扁平
化成一个流。这样你就得到了一个三元数流。还要注意,我们把 b 的范围改成了 a 到100。没有必要再从1开始了,否则就会造成
重复的三元数,例如(3,4,5)和(4,3,5)。
7. 运行代码
现在你可以运行解决方案,并且可以利用我们前面看到的 limit 命令,明确限定从生成的流中要返回多少组勾股数了:
pythagoreanTriples.limit(5)
.forEach(t -> System.out.println(t[0] + ", " + t[1] + ", " + t[2]));
这会打印:
3, 4, 5
5, 12, 13
6, 8, 10
7, 24, 25
8, 15, 17
8. 你还能做得更好吗?
目前的解决办法并不是最优的,因为你要求两次平方根。让代码更为紧凑的一种可能的方法是,先生成所有的三元数
(a*a, b*b, a*a+b*b) ,然后再筛选符合条件的:
Stream<double[]> pythagoreanTriples2 =
IntStream.rangeClosed(1, 100).boxed()
.flatMap(a ->
IntStream.rangeClosed(a, 100)
.mapToObj(
b -> new double[]{a, b, Math.sqrt(a*a + b*b)})
.filter(t -> t[2] % 1 == 0));
