【luoguP1086】【2004NOIP-Ua】花生采摘

P1086 花生采摘

题目描述

鲁宾逊先生有一只宠物猴，名叫多多。这天，他们两个正沿着乡间小路散步，突然发现路边的告示牌上贴着一张小小的纸条：“欢迎免费品尝我种的花生！――熊字”。

鲁宾逊先生和多多都很开心，因为花生正是他们的最爱。在告示牌背后，路边真的有一块花生田，花生植株整齐地排列成矩形网格（如图1）。有经验的多多一眼就能看出，每棵花生植株下的花生有多少。为了训练多多的算术，鲁宾逊先生说：“你先找出花生最多的植株，去采摘它的花生；然后再找出剩下的植株里花生最多的，去采摘它的花生；依此类推，不过你一定要在我限定的时间内回到路边。”

我们假定多多在每个单位时间内，可以做下列四件事情中的一件：

1) 从路边跳到最靠近路边（即第一行）的某棵花生植株；

2) 从一棵植株跳到前后左右与之相邻的另一棵植株；

3) 采摘一棵植株下的花生；

4) 从最靠近路边（即第一行）的某棵花生植株跳回路边。

现在给定一块花生田的大小和花生的分布，请问在限定时间内，多多最多可以采到多少个花生？注意可能只有部分植株下面长有花生，假设这些植株下的花生个数各不相同。

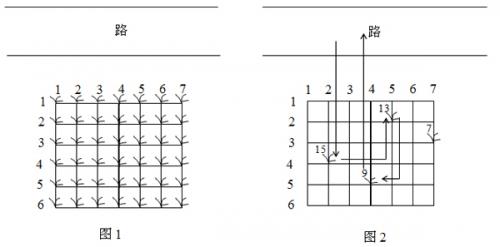
例如在图2所示的花生田里，只有位于(2, 5), (3, 7), (4, 2), (5, 4)的植株下长有花生，个数分别为13, 7, 15, 9。沿着图示的路线，多多在21个单位时间内，最多可以采到37个花生。

输入输出格式

输入格式：

 

输入文件peanuts.in的第一行包括三个整数，M, N和K，用空格隔开；表示花生田的大小为M * N（1 <= M, N <= 20），多多采花生的限定时间为K（0 <= K <= 1000）个单位时间。接下来的M行，每行包括N个非负整数，也用空格隔开；第i + 1行的第j个整数Pij（0 <= Pij <= 500）表示花生田里植株(i, j)下花生的数目，0表示该植株下没有花生。

 

输出格式：

 

输出文件peanuts.out包括一行，这一行只包含一个整数，即在限定时间内，多多最多可以采到花生的个数。

 

输入输出样例

输入样例1：

6 7 21
0 0 0 0 0 0 0
0 0 0 0 13 0 0
0 0 0 0 0 0 7
0 15 0 0 0 0 0
0 0 0 9 0 0 0
0 0 0 0 0 0 0

输出样例1：

37

输入样例2：

6 7 20
0 0 0 0 0 0 0
0 0 0 0 13 0 0
0 0 0 0 0 0 7
0 15 0 0 0 0 0
0 0 0 9 0 0 0
0 0 0 0 0 0 0

输出样例2：

28

说明

noip2004普及组第2题

这道题可以用深搜来做，当然，由于数据比较水，所以用模拟也是完全可以AC的，在这里给大家介绍一种DFS+模拟的做法。

首先，我们要搞明白几个事情：

1.这不是一道动规题目！题目中有一个点很多人都没有看到：这个题要求猴子那花生数从大到小采摘，所以猴子的动向是固定的，而不是按你的思路让猴子在一定时间内摘到最多的花生。

2.中途不可以回到路边！一些聪明的小朋友不难想到：猴子还可以在中途先回到大路上，因为按题目理解，在路上并不需要花费时间。

但对于这个题是不可行的，Yeasion曾经亲身试验过，然后完美爆零。。。。。。

然后就是这个题的思路了，我们从最大的点开始，不断深搜下一大的点，然后将猴子瞬移过去，对你没有看错，是瞬移，而不是一格一格地走，在瞬移之后，我们将猴子现在花费了的时间加上达到那个点所要花费的时间，然后只要判断一下现在花费的时间是不是大于等于限定的时间就可以了。如果是的话就直接break，不是的话就继续深搜。当然在深搜的过程当中需要定义一个maxn点和maxni,maxnj分别是最大的花生植株及其横纵坐标，当然，在采摘过之后我们还要把这个植株上面的花生数量清零，防止重复搜索。

好的那么接下来附上代码：：

#include<cmath>
#include <cmath>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int m,n,k,ans=0;
int a[25][25];
void dfs(int x,int y,int time)
{
    int Max=-(1<<30),nx,ny;
    //Max最大的花生点
    //nx最大花生点的x坐标
    //ny最大花生点的y坐标
    for(int i=1;i<=m;i++)
        for(int j=1;j<=n;j++)
            if(a[i][j]>Max)
            {
                Max=a[i][j];
                nx=i;
                ny=j;
                //更新
            }
    if(y==0) y=ny;//边界
    int nt=abs(nx-x)+abs(ny-y)+nx+1;
    //如果采这一棵花费的时间
    if(time<nt || a[nx][ny]==0) return;
    //边界返回条件
    else
    {
        ans+=a[nx][ny];
        //可以选择，ans更新
        a[nx][ny]=0;
        dfs(nx,ny,time-abs(nx-x)-abs(ny-y)-1);
    }
}

int main()
{
    scanf("%d %d %d",&m,&n,&k);
    for(int i=1;i<=m;i++)
        for(int j=1;j<=n;j++)
            scanf("%d",&a[i][j]);
    dfs(0,0,k);
    printf("%d
",ans);
    return 0;
}