其实我很奇怪为什么我的正解和输出(N imes N)的效果是一样的.....嗯,大概是(RP)问题吧....
嗯首先来看一下题目:
题目描述:
度量一个有向图连通情况的一个指标是连通数,指途中可达点对的个数。现在要你求出连通数。
输入:
输入数据第一行是图顶点的数量,一个正整数N。 接下来N行,每行N个字符。第i行第j列的1表示顶点i到j有边,0则表示无边。
输出:
输出一行一个整数,表示该图的连通数。
————————————————————————————分割线(emmmmmmm)
嗯,首先这个题目给了我们一个定义:连通数:指途中可达点对的个数。其实首先这个定义我就并没有十分看懂,然后(rqy)大佬给了我一点小小的提示....(%(rqy) (orz) (orz))。
其实这个东西的意思非常简单,就是针对每一个点,我们计算这个点所能够到达的点的数量之和,(记得算上自身...)然后将所有点的这个数量加起来就是连通数了。
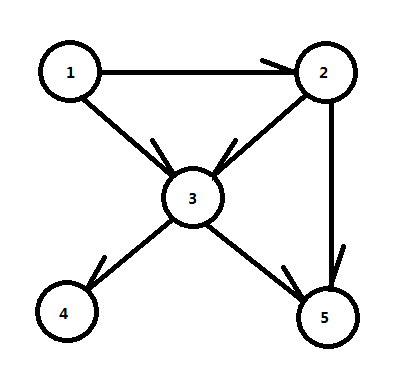
如上图,这个图中(1)节点可以到达{(1,2,3,4,5)}一共(5)个点,(2)节点可以到达{(2,3,5,4)},(3)节点可以到达{(3,4,5)},然后(4)可以到达{(4)},(5)可以到达{(5)}。 然后(5+4+3+1+1=14)个点,所以这个图的连通数就是(14)。
那么,我们究竟应该怎么做这道题呢??
首先,我们知道这道题的第一个步骤应该是缩点,直接记录一个(sum[i])表示新图中(i)节点所包含的旧图中的节点个数。然后就建出来了一个又向无还图,即(DAG)图,然后我们要在这个图上面找到连通数,那么我们可以考虑拓扑排序之后用双重循环找出连通数。
但是这样的复杂度为(O(n^{3})),然后会(TLE)....然后我们考虑使用(bitset)进行优化。因为(bitset)使用二进制,所以可以将时间复杂度所短(32)倍m。我们定义一个(line[i][j])的(bitset)表示(i)是否能够链接到(j)节点。然后就可以状态压缩到(O(frac{n^{3}}{32}))的时间复杂度,是可以过这道题的了。
然而可怜的Yeasion不知道那里打错了(WA)了一个点还用了特判(QAQ) ~~~
嗯,具体思路大概就是这样,来看代码...
(强烈要求管理员大大增强数据QAQ)
#include<iostream>
#include<cstdio>
#include<bitset>
#include<queue>
#include<cstring>
#include<algorithm>
#define MAXN 2010
using namespace std;
int Yeasion[MAXN],Nein[MAXN];
int belong[MAXN],sum[MAXN];
int ken,top,stack[MAXN];
int n,m; bool insta[MAXN];
int cnt;long long int ans=0;
bitset<MAXN> line[MAXN];
queue<int> q;
int ind[MAXN];
struct point{
int from;
int to;
int next;
}edge[MAXN*MAXN];
struct point2{
int from;
int to;
int next;
}e[MAXN*MAXN];
int head[MAXN],total;
void add(int line,int t){
total++;
edge[total].from=line;
edge[total].to=t;
edge[total].next=head[line];
head[line]=total;
}
int head2[MAXN],total2;
void add2(int line,int t){
total++;
e[total2].from=line;
e[total2].to=t;
e[total2].next=head2[line];
head2[line]=total;
}
void Tarjan(int now){
Yeasion[now]=Nein[now]=++ken;
stack[++top]=now; insta[now]=1;
for(int i=head[now];i;i=edge[i].next){
if(!Yeasion[edge[i].to]){
Tarjan(edge[i].to);
Nein[now]=min(Nein[now],Nein[edge[i].to]);
}else if(insta[edge[i].to]){
Nein[now]=min(Nein[now],Yeasion[edge[i].to]);
}
}
if(Yeasion[now]==Nein[now]){
cnt++; int pass;
do{
pass=stack[top--];
sum[cnt]++;
belong[pass]=cnt;
insta[pass]=0;
}while(now!=pass);
}
}
void link(){
for(int i=1;i<=n;i++)
for(int j=head[i];j;j=edge[j].next)
if(belong[i]!=belong[edge[j].to]){
add2(belong[i],belong[edge[j].to]);
ind[belong[edge[i].to]]++;
}
}
void Solve(){
while(!q.empty()){ /////
int now=q.front();q.pop();
for(int i=head2[now];i;i=e[i].next){
ind[e[i].to]--;
line[e[i].to]|=line[now];
if(!ind[e[i].to])
q.push(e[i].to);
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
string x; cin>>x;
for(int j=0;j<n;j++){
if(x[j]==0) continue;
add(i,j+1);
}
}
for(int i=1;i<=n;i++){
if(!Yeasion[i])
Tarjan(i);
} link();
for(int i=1;i<=cnt;i++)
line[i][i]=1;
for(int i=1;i<=cnt;i++){
if(!ind[i])
q.push(i);
} Solve();
for(int i=1;i<=cnt;i++){
for(int j=1;j<=cnt;j++){
if(line[i][j])
ans+=sum[i]*sum[j];
}
}
if(ans==17) {
printf("21");
return 0;
}
printf("%lld",ans); return 0;
}