最短路径问题：弗洛伊德算法（Floyd）

Floyd算法

1.定义概览

Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N³)，空间复杂度为O(N²)。

 

2.算法描述

1)算法思想原理：

     Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）

      从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

2).算法描述：

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 　　

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

3).Floyd算法过程矩阵的计算----十字交叉法

方法：两条线，从左上角开始计算一直到右下角 如下所示

给出矩阵，其中矩阵A是邻接矩阵，而矩阵Path记录u,v两点之间最短路径所必须经过的点

 

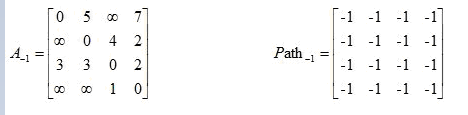
相应计算方法如下：

 

 

最后A₃即为所求结果。

【例题】：最短路问题

【问题描述】：

　　平面上有n（n<=100），每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。

　　若有连线，则表示可以从一个点到达另一个点，即两个点之间有通路，通路的距离为两点之间的距离，现在的任务是找出从一点到另一个点的最短距离。

【输入格式】：

第一行：n。

第二行到第n+1行：每行两个整数，描述了一个点的坐标。

第n+2行为一个整数m，表示图中的连线的个数。

此后的m行，每行一个连线，有两个整数i和j组成，表示第i 和j个点之间有连线。

最后一行：两个整数：s，t，分别表示起点和终点的坐标。

【输出格式】：

一个整数表示从s到t的最短路的距离。

【输入样例】：

5

0 0

2 0

2 2

0 2

3 1

5

1 2

1 3

1 4

2 5

3 5

1 5

【输出样例】：3.41

【参考程序】：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
int a[101][3];
double f[101][101];
int n,i,j,x,y,k,m,s,e;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    cin>>a[i][1]>>a[i][2];
    cin>>m;
    memset(f,0x7f,sizeof)
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        f[y][x]=f[x][y]=sqrt(pow(a[x][1]-a[y][1],2)+pow(double(a[x][2]-a[y][2]),2));
    }
    cin>>s>>e;
    for(int k=1;k<=n;k++)
     for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
       if(i!=j)&&(i!=k)&&(k!=j)
        if(f[i][k]+f[k][j]<f[i][j])
         f[i][j]=f[i][k]+f[k][j];
    printf("%.2lf
",,f[s][e]);
    return 0;
}