题目描述:
期末考试考完了,分数也出来了,大家准备吃糖庆祝一下,为了鼓励同学们下学期能取得更好的成绩,司马红豆同学让n个同学站成一排,如果某个同学的分数比相邻的一个同学要高,那么他得到的糖果就会比这个分数较低的相邻的同学多,每个人至少能得到一个糖果。现在司马红豆想要知道最少需要多少个糖果能完成分糖任务。
输入格式:
第一行输入一个整数n, (1≤n≤100000)
第二行输入n 个整数,依次表示排成一排后每位同学的分数ai, (1≤ai≤1000)。
输出格式:
输出一个整数,表示最少需要的糖果数量
样例输入1:
3
1 0 2
样例输出1:
5
样例输入2:
3
1 2 2
样例输出2:
4
题解:这题乍一看就感觉要抽象成图论模型
将小的数建一条指向大的数的边,建完边你会得到这样的东西
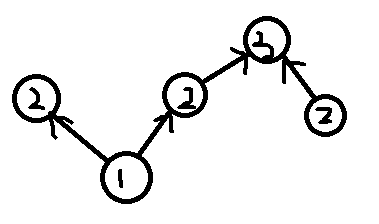
显然一个点所需要的最大糖数是所有入度为零的点到他的最大距离+1,记为f[i]
所以枚举每一个入度为零的点,从他开始更新每一个能到达的的点的f[i]
最后将每个点的f[i]加起来即为答案
虽然看着好像因为没有vis之类的东西,每个点会被访问很多遍,但是其实每个点最多只会被两个点向指,所以复杂度大约是O(n)的
大概有点dp的思想?
代码如下:
#include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int d[100010],n,a[100010],f[100010]; long long ans=0; vector<int> g[100010]; void dfs(int now,int deep) { f[now]=max(f[now],deep); for(int i=0;i<g[now].size();i++) { dfs(g[now][i],deep+1); } } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } for(int i=2;i<=n;i++) { if(a[i-1]>a[i]) { g[i].push_back(i-1); d[i-1]++; } if(a[i]>a[i-1]) { g[i-1].push_back(i); d[i]++; } } for(int i=1;i<=n;i++) { if(!d[i]) { dfs(i,1); } } for(int i=1;i<=n;i++) { ans+=f[i]; } printf("%d ",ans); }