“队列进出图上的方向
线段树区间修改求出总量
可持久留下的迹象
我们 俯身欣赏” ----《膜你抄》
线段树很早就会写了,但一直没有总结,所以偶尔重写又会懵逼,所以还是要总结一下。
引言
在生活和竞赛中,我们总是会遇上一些问题,比如说令人厌恶的统计成绩,老师会想询问几个人中成绩最低的是谁......
于是问题出现了。
e.g.1(暴力膜不可取)
已知班上有50个学生,学号分别为1-50,老师想问学号为a-b之间的最低分是多少
比如 2 5 3 4 1中 2-4 之间的最小值为 3
显然数据非常少,我们可以针对每个询问,扫一遍,获得最小值。
复杂度呢?假设有m个询问,a-b的区间最大为n
所以复杂度为Θ(mn)。
e.g.2(st表)
那么新问题来了,一场多市联考以后,你的老师拿到了一份有100000人成绩的表格(并没有任何科学依据,纯属胡诌,如有雷同,不胜荣幸),老师现在想问你a-b之间的最低分是多少,并在一秒内出解。
说句实话老师你为什么一定要在1秒内出解啊
反正就当老师赶时间吧(摊手)
因为是静态查询,我们可以用st表来做,这就不详细说了。
复杂度为Θ(询问次数),但预处理是Θ(nlogn)的。
代码如下:
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,m,dp[100010][17]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%d",&dp[i][0]); } for(int i=1;i<=17;i++) { for(int j=1;j<=n;j++) { if(j+(1<<(i-1))-1<=n) { dp[j][i]=min(dp[j][i-1],dp[j+(1<<(i-1))][i-1]); } } } int l,r; for(int i=1;i<=m;i++) { scanf("%d%d",&l,&r); int x=(int)(log((double)(r-l+1))/log(2.0)); printf("%d ",min(dp[l][x],dp[r-(1<<x)+1][x])); } }
e.g.3(线段树点修改)
成绩还在复查,有时候会偶尔发现有些同学的成绩算错了,然后要更新,于是老师又会想要询问a~b之间的最低分,还是100000个学生.......
说句实话老师你难道不能等到复查完再查分吗
这道题和e.g.2有什么区别吗?
这道题是强制在线的,因为一个同学的成绩改变以后会导致整个区间的值改变。
这样st表就失效了。
我们会发现st表在查询上很优,但构造的话就.......
那有没有什么好的办法呢?
虽然st表有点小问题,但它的思想可以借鉴——两个小区间中最小值较小的那个是这个大区间的最小值。
那么不妨想一想
如果一个数值修改了,st表的哪些部分需要改动呢?
如果这些改动的部分并不多,我们可以只改这些部分,就不用重构st表了!
不用想自然是所有覆盖这个点的区间。
这些区间有多少呢?长度为一的一个,为二的两个,为四的四个.......加起来似乎太多了!与其如此,我还不如重构st表呢!
好的,那么如今的问题就变成了,该怎么让这些区间变得少一些。
继续开始yy,我们的一个点在一个二的幂次的长度上只出现一次,那么样这一个点要修改值的时候,我们只用修改包含它长度为2,4,8.....的点就可以了。
那么这是什么呢?一棵二叉树。
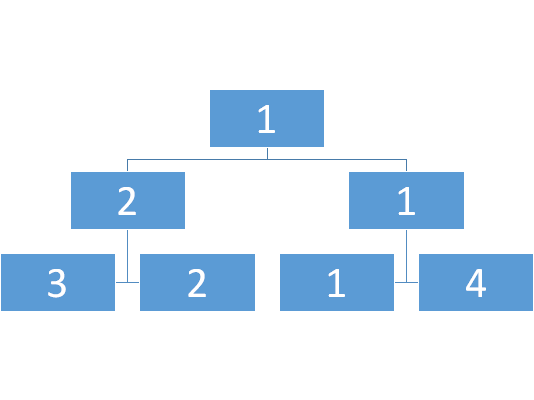
好的吧 上面的似乎是错的,因为如果有不是2的幂次,树就建不起来了。
那么索性逆其道而行,我们靠二分长度来建树。
数值树:
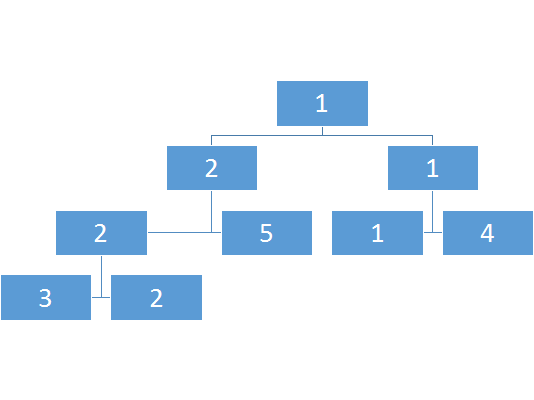
区间树:
那么此时建出来的树中如果要修改一个点的怎么办呢
很简单,修改它所有的影响的父节点就行了
嘛,当然不是每个父节点都要改,还是要按题意来的啊~
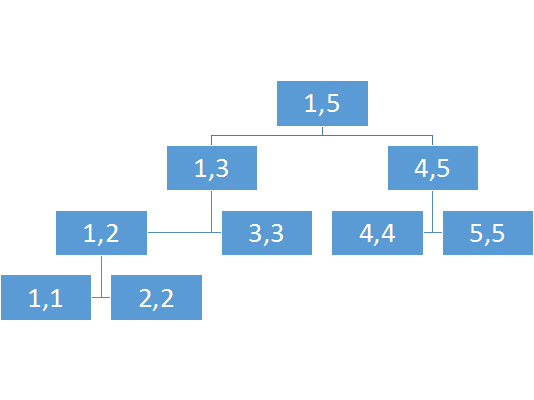
比如这个:

那么怎么查询呢?
比如说我要查询上图2-4的最小值
但是会发现2-4并没有完整对应的区间,如果有的话自然是能直接出解
那怎么办呢?
我们可以通过二分确定长度的中间值,然后判断我们的查询的l是否小于mid,如果是,那么这个节点的左子树中有一部分解会影响到总解,我们需要继续搜这颗子树的子树,最终如果对于一个子树它的l-r被a-b所包含,那么就不用再搜了。
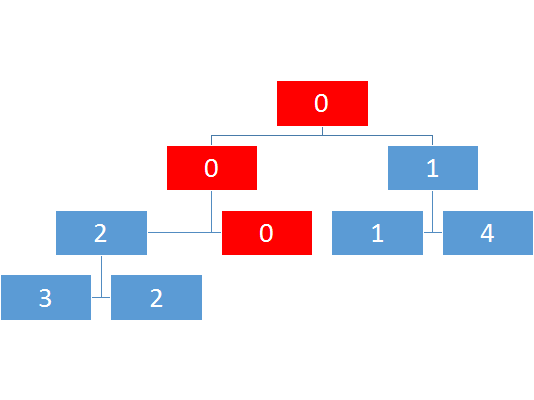
比如查询区间2-4
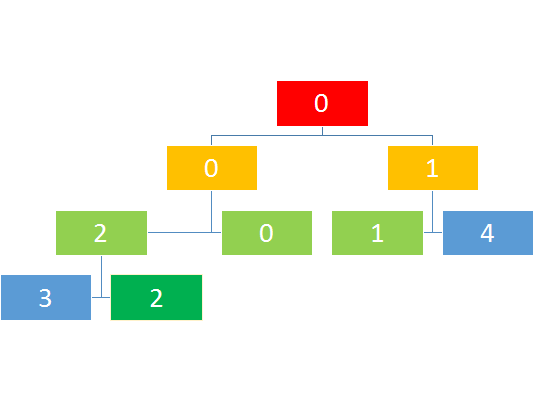
如图则是查询访问的次序。
那么它的复杂度是多少呢?
显然建树是Θ(nlogn)修改是Θ(logn)
那么查询呢?
可以想象,对于一个区间,他一定包含一个长度小于他的最长的2的幂次的长度,比如说长度为十的区间中一定包含一个长度为八的区间
这个区间如果刚好对应一个相应的节点,那么它就相当于用了一的费用,查了八个解
但比较尬的是有时候这个八是被错开的,但再不济也能分成两个四,相当于用了二的费用查了八个解
那么对于这个区间每次最多需要用二的费用除掉最大的二的幂次的解
我们知道1+2+4+8+......+2^n=2^(n+1)-1
而在2^(n+1)-1的范围内所有的数字都能用最多n个2的幂次之和表示
所以复杂度为Θ(logn)
e.g.3.1线段树点修改如何实现?
似乎可以理解线段树的思想了,但其实还是一脸懵逼(其实我估计一般人看不懂……)
那么就详细的拆开来讲讲吧。
建树(build)
好的,那么应该怎么建树呢?
我们需要快速的查询二叉树的每个点的父节点和子节点,同是内存还要尽可能省,我们可以对于一个编号为n的点将它的父节点记为[n/2](取整),左儿子记为2*n,右儿子记为2*n+1
然后根节点为1,表示1-n区间中所要求的值(按题意来定)
这样子不会有冲突,因为一个深度n的树最多有2^n-1个节点,而深度为n+1的标号最小的子树为2^n。
然后建树从叶子节点开始,逐渐传到父节点,所以我们还需要一个函数(push_up),来计算两个子节点到父节点的转移。
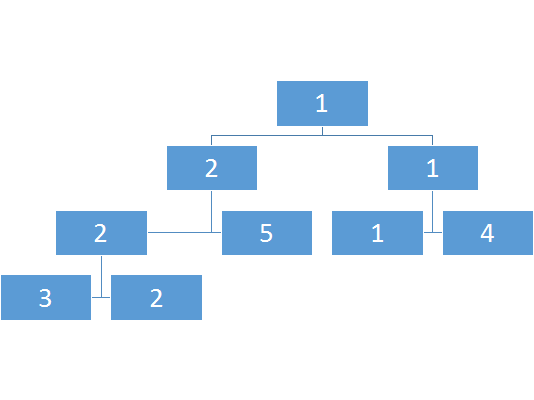
当然实际建树是dfs的,反正理解一发就行了!
主要需要两个函数:push_up,build
1、push_up

2、build
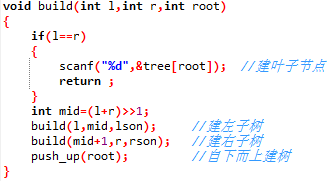
点更新(update)
自然是先更新那个点,然后更新他的所有父节点。
update
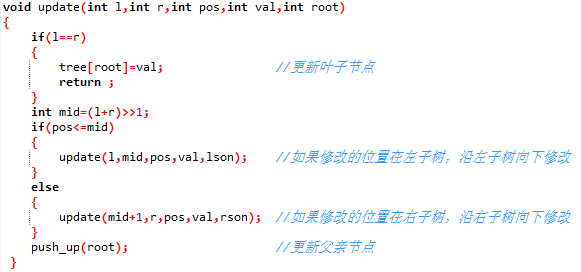
查询(query)
按照之前的解释已经说的很清楚了
query

这样子点修改的线段树就基本写出来了
那么来一道例题
hdu1754 i hate it
有n个数,m个操作,操作分为两种种类:
1、Q l r 询问l-r之间最大值
2、U x v 将x位置的值换成当前值与v值中较大的一个
输入样例#1:
5 6
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 2 9
Q 1 5
输出样例#1:
5
6
5
9
代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define lson root<<1 #define rson root<<1|1 int tree[800010],n,m,a,b,x,v; char c; void push_up(int root) { tree[root]=max(tree[lson],tree[rson]); } void build(int l,int r,int root) { if(l==r) { scanf("%d",&tree[root]); return ; } int mid=(l+r)>>1; build(l,mid,lson); build(mid+1,r,rson); push_up(root); } void update(int l,int r,int x,int v,int root) { if(l==r) { tree[root]=max(tree[root],v); return; } int mid=(l+r)>>1; if(x<=mid) { update(l,mid,x,v,lson); } else { update(mid+1,r,x,v,rson); } push_up(root); } int query(int a,int b,int l,int r,int root) { int ans=0; if(l>=a&&b>=r) { return tree[root]; } int mid=(l+r)>>1; if(a<=mid) { ans=max(ans,query(a,b,l,mid,lson)); } if(mid<b) { ans=max(ans,query(a,b,mid+1,r,rson)); } return ans; } int main() { while(scanf("%d%d",&n,&m)!=EOF) { build(1,n,1); for(int i=1; i<=m; i++) { scanf(" %c",&c); if(c=='Q') { scanf("%d%d",&a,&b); printf("%d ",query(a,b,1,n,1)); } if(c=='U') { scanf("%d%d",&x,&v); update(1,n,x,v,1); } } } return 0; }
当然也可以用结构体来储存树的结构,比如区间的左和右端点,这样子可以少传递几个参数,不过实际上速度并不会快很多,甚至会慢……不过这有什么问题吗,这玩意可能会更加好写2333
代码:
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define lson root<<1 #define rson root<<1|1 using namespace std; struct node { int l,r,m; } tr[800080]; int n,m; void push_up(int root) { tr[root].m=max(tr[lson].m,tr[rson].m); } void build(int root,int l,int r) { if(l==r) { tr[root].l=l; tr[root].r=r; scanf("%d",&tr[root].m); return ; } tr[root].l=l; tr[root].r=r; int mid=(l+r)>>1; build(lson,l,mid); build(rson,mid+1,r); push_up(root); } void update(int root,int pos,int val) { if(tr[root].l==pos&&tr[root].r==pos) { tr[root].m=max(tr[root].m,val); return ; } int mid=(tr[root].l+tr[root].r)>>1; if(pos<=mid) { update(lson,pos,val); } else { update(rson,pos,val); } push_up(root); } int query(int root,int l,int r) { if(l==tr[root].l&&r==tr[root].r) { return tr[root].m; } int mid=(tr[root].l+tr[root].r)>>1; if(l>mid) { return query(rson,l,r); } else { if(mid>=r) { return query(lson,l,r); } else { return max(query(lson,l,mid),query(rson,mid+1,r)); } } } int main() { while(scanf("%d%d",&n,&m)!=EOF) { build(1,1,n); while(m--) { char kd; scanf(" %c",&kd); if(kd=='Q') { int l,r; scanf("%d%d",&l,&r); printf("%d ",query(1,l,r)); } if(kd=='U') { int pos,val; scanf("%d%d",&pos,&val); update(1,pos,val); } } } }
上面那题为单点修改求区间最大值模板
那么我们再来一道单点修改求区间和模板题
给出n个点以及一些操作,操作分为四种
1、Add x v 给x的位置加v
2、Sub x v 给x的位置减v
3、Query l r 求l-r的区间和
4、End 结束询问
Sample Input
1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
Sample Output
Case 1:
6
33
59
代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define lson root<<1 #define rson root<<1|1 int tree[800010],n,m,a,b,x,v; char c[10]; void push_up(int root) { tree[root]=tree[lson]+tree[rson]; } void build(int l,int r,int root) { if(l==r) { scanf("%d",&tree[root]); return ; } int mid=(l+r)>>1; build(l,mid,lson); build(mid+1,r,rson); push_up(root); } void update(int l,int r,int x,int v,int root) { if(l==r) { tree[root]+=v; return; } int mid=(l+r)>>1; if(x<=mid) { update(l,mid,x,v,lson); } else { update(mid+1,r,x,v,rson); } push_up(root); } int query(int a,int b,int l,int r,int root) { int ans=0; if(l>=a&&b>=r) { return tree[root]; } int mid=(l+r)>>1; if(a<=mid) { ans+=query(a,b,l,mid,lson); } if(mid<b) { ans+=query(a,b,mid+1,r,rson); } return ans; } int main() { int t,ttt=0; scanf("%d",&t); while(t--) { ttt++; printf("Case %d: ",ttt); memset(tree,0,sizeof(tree)); scanf("%d",&n); build(1,n,1); while(1) { cin>>c; if(c[0]=='Q') { scanf("%d%d",&a,&b); printf("%d ",query(a,b,1,n,1)); } if(c[0]=='A') { scanf("%d%d",&x,&v); update(1,n,x,v,1); } if(c[0]=='S') { scanf("%d%d",&x,&v); update(1,n,x,-v,1); } if(c[0]=='E') { break; } } } return 0; }
自然也可以写结构体板的,但请容我偷个懒哈~(doge)
不不不不,偷懒其实是为了写下面这道好题。
可以说如果下面这道题能写出来,就说明你对线段树的结构有一定的了解了。
洛谷U23283(原题为codeforces 914D,这款游戏就不要玩了,太伤身体)
题目大意
给出一段序列,两个操作
操作1 给出l,r,x
求区间l-r的gcd,如果至多能改掉区间内的一个数(不影响原序列),使gcd是x的倍数,那么输出YES,否则输出NO
操作2 给出pos,x
将序列中pos位置上的数字改为x
首先GCD是具有传递性的,所以可以使用线段树进行维护,但比较麻烦的就是可以改掉一个数。
可以试想一下,对于每个区间的查询,我们最终得到的是若干完整返回块的gcd,如果其中有两个块gcd都不是x的倍数,那么肯定GG
如果只有一个块不是呢?这个块中也可能有多个数不是x的倍数,还需要再检验一下。
线段树的思路就是一个节点的数值由他的两个儿子节点转移而来,如果他的两个儿子节点的gcd都不是x的倍数,那么还是GG
如果只有一个不是,我们就继续查看那个点的左右儿子gcd是否都不是x的倍数,直到长度为一的节点即可,此时一定满足条件
每次可以去掉一半的长度,相当于二分。
算上gcd带的log的情况下,复杂度为Θ(n*logn*logn)。
代码如下:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define lson root<<1 #define rson root<<1|1 using namespace std; int gcd(int a,int b) { if(b>a) { swap(a,b); } if(b) { return gcd(b,a%b); } else { return a; } } int nowson,x,cnt,n,m; struct node { int l,r,g; }tr[2000020]; void push(int root) { tr[root].g=gcd(tr[rson].g,tr[lson].g); } void build(int root,int l,int r) { if(l==r) { tr[root].l=l; tr[root].r=r; scanf("%d",&tr[root].g); return ; } int mid=(l+r)>>1; tr[root].l=l; tr[root].r=r; build(lson,l,mid); build(rson,mid+1,r); push(root); } void update(int root,int pos,int v) { if(tr[root].l==pos&&tr[root].r==pos) { tr[root].g=v; return ; } int mid=(tr[root].l+tr[root].r)>>1; if(mid>=pos) { update(lson,pos,v); } else { update(rson,pos,v); } push(root); } int query(int root,int l,int r) { if(tr[root].l==l&&tr[root].r==r) { if(tr[root].g%x!=0) { cnt--; nowson=root; } return tr[root].g; } int mid=(tr[root].l+tr[root].r)>>1; if(l>mid) { return query(rson,l,r); } else { if(r<=mid) { return query(lson,l,r); } else { return gcd(query(lson,l,mid),query(rson,mid+1,r)); } } } int check(int root) { if(tr[root].l==tr[root].r) { return 1; } if(tr[lson].g%x!=0&&tr[rson].g%x!=0) { return 0; } if(tr[lson].g%x==0) { return check(rson); } else { return check(lson); } } int main() { int n,m; scanf("%d",&n); build(1,1,n); scanf("%d",&m); for(int i=1;i<=m;i++) { int kd,l,r; scanf("%d",&kd); if(kd==1) { cnt=1; scanf("%d%d%d",&l,&r,&x); int tmp=query(1,l,r); if(x==tmp) { puts("YES"); } else { if((!cnt)&&check(nowson)) { puts("YES"); } else { puts("NO"); } } } else { scanf("%d%d",&l,&r); update(1,l,r); } } }
e.g.4(线段树区间修改)
复查时出现了评卷大错误,连续一个考场某道题的分都没有加,现在需要给加上,然后老师把聪明的你推荐给了统分人(作了吧233)要询问区间和以方便计算平均数。
好的吧,反正改一个也是改,改一段也是改。
来看一道例题
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x(区间加)
2.求出某区间每一个数的和(区间求和)
最简单的思路自然是给每个点都加上值然后push_up
代码:
#include<cstdio> #include<vector> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define lson root<<1 #define rson root<<1|1 long long tree[400040]; int n,m; void push_up(int root) { tree[root]=tree[lson]+tree[rson]; } void build(int l,int r,int root) { if(l==r) { scanf("%lld",&tree[root]); return; } int mid=(l+r)>>1; build(l,mid,lson); build(mid+1,r,rson); push_up(root); } void add(int l,int r,int root,int ls,int rs,int v) { if(l==r) { tree[root]+=v; return; } int mid=(l+r)>>1; if(ls<=mid) { add(l,mid,lson,ls,rs,v); } if(rs>mid) { add(mid+1,r,rson,ls,rs,v); } push_up(root); } long long query(int l,int r,int ls,int rs,int root) { if(l>=ls&&r<=rs) { return tree[root]; } int mid=(l+r)>>1; long long ans=0; if(ls<=mid) { ans+=query(l,mid,ls,rs,lson); } if(rs>mid) { ans+=query(mid+1,r,ls,rs,rson); } return ans; } int main() { int n,m; scanf("%d%d",&n,&m); build(1,n,1); for(int i=1;i<=m;i++) { int kd; int l,r,v; scanf("%d",&kd); if(kd==1) { scanf("%d%d%d",&l,&r,&v); add(1,n,1,l,r,v); } if(kd==2) { scanf("%d%d",&l,&r); int ans=query(1,n,l,r,1); printf("%lld ",ans); } } }
然后就光荣的TLE了,我们考虑再优化一发
其实完全不用每个点push_up
因为我们完全可以用l-r区间中包含的需要修改的点的个数来算出该区间需要加上的值,即为修改点个数乘以每个点修改的值。
这样子可以省掉不少时间,因为将加法变成乘法后原本复杂度为Θ(长度)的加就变成了Θ(1)的乘
代码:
#include<cstdio> #include<vector> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define lson root<<1 #define rson root<<1|1 long long tree[400040]; int n,m; void push_up(int root) { tree[root]=tree[lson]+tree[rson]; } void build(int l,int r,int root) { if(l==r) { scanf("%lld",&tree[root]); return; } int mid=(l+r)>>1; build(l,mid,lson); build(mid+1,r,rson); push_up(root); } void add(int l,int r,int root,int ls,int rs,int v) { if(l==r) { tree[root]+=v; return; } int mid=(l+r)>>1; if(ls<=mid) { add(l,mid,lson,ls,rs,v); } if(rs>mid) { add(mid+1,r,rson,ls,rs,v); } push_up(root); } long long query(int l,int r,int ls,int rs,int root) { if(l>=ls&&r<=rs) { return tree[root]; } int mid=(l+r)>>1; long long ans=0; if(ls<=mid) { ans+=query(l,mid,ls,rs,lson); } if(rs>mid) { ans+=query(mid+1,r,ls,rs,rson); } return ans; } int main() { int n,m; scanf("%d%d",&n,&m); build(1,n,1); for(int i=1;i<=m;i++) { int kd; int l,r,v; scanf("%d",&kd); if(kd==1) { scanf("%d%d%d",&l,&r,&v); add(1,n,1,l,r,v); } if(kd==2) { scanf("%d%d",&l,&r); int ans=query(1,n,l,r,1); printf("%lld ",ans); } } }
但是因为每一个修改的叶节点的父节点及祖先节点都需要遍历,复杂度似乎还有点可怕(但比起之前快了近两倍)
所以又一次光荣的TLE了
但是这次计算中的乘思想是比较有启发的。
那该怎么继续优化呢?
ちょっとまって!我们之前的查询为什么是Θ(logN)的呢?
我们可以发现,其实查询的时候我们遵循能返回大块就返回大块的思路,不会再下去查询小块
而我们却在每次更新时都会去将所有的大块和小块一并更新,
那么能不能只更新大块呢?
显然不行
因为我们仍然可能会需要查询一些更小的区间的值。
但是我们可以退而求其次,等到需要查找更小的区间的时候再去更新
于是就可以给每一个点打上一个标记,等我们访问了他的父节点再将他的父节点附上这个值,并将这个值向下推给他,这就是lazy-tag的思想。
需要一个新的函数:用于将懒惰标记下传。
push_down

当然原来的其他函数也要有所改动,具体看代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define lson root<<1 #define rson root<<1|1 using namespace std; struct node { long long l,r,sum,lazy; }tree[400040]; int n,m,kd; void push_up(int root) { tree[root].sum=tree[lson].sum+tree[rson].sum; } void push_down(int root) { int mid=(tree[root].l+tree[root].r)>>1; tree[lson].sum+=tree[root].lazy*(mid-tree[root].l+1); tree[rson].sum+=tree[root].lazy*(tree[root].r-mid); tree[lson].lazy+=tree[root].lazy; tree[rson].lazy+=tree[root].lazy; tree[root].lazy=0; } void build(int l,int r,int root) { if(l==r) { tree[root].l=l; tree[root].r=r; scanf("%lld",&tree[root].sum); return; } tree[root].l=l; tree[root].r=r; int mid=(l+r)>>1; build(l,mid,lson); build(mid+1,r,rson); push_up(root); } void add(int l,int r,int root,int x) { if(l==tree[root].l&&r==tree[root].r) { tree[root].lazy+=x; tree[root].sum+=x*(tree[root].r-tree[root].l+1); return; } int mid=(tree[root].l+tree[root].r)>>1; if(tree[root].lazy) { push_down(root); } if(r<=mid) { add(l,r,lson,x); } else { if(l>mid) { add(l,r,rson,x); } else { add(l,mid,lson,x); add(mid+1,r,rson,x); } } push_up(root); } long long query(int l,int r,int root) { if(l==tree[root].l&&tree[root].r==r) { return tree[root].sum; } int mid=(tree[root].l+tree[root].r)>>1; if(tree[root].lazy) { push_down(root); } if(r<=mid) { return query(l,r,lson); } else { if(l>mid) { return query(l,r,rson); } } return query(l,mid,lson)+query(mid+1,r,rson); } int main() { scanf("%d%d",&n,&m); build(1,n,1); for(int i=1;i<=m;i++) { scanf("%d",&kd); if(kd==1) { int l,r,x; scanf("%d%d%d",&l,&r,&x); add(l,r,1,x); } else { int l,r; scanf("%d%d",&l,&r); printf("%lld ",query(l,r,1)); } } }
这就是lazy标记比较浅薄的应用,我们可以再来看一道比较抽象的题目
题目大意:
在墙上按照输入顺序贴海报,求最后能看见几张不同的海报
emmm,这道题要用离散化的思路,因为原来的区间实在是太大了!
这是也我选这道题的唯一原因
至于倒贴海报什么的我倒是不敢苟同,因为明显有更加暴力的方法啊……
来来来,让我们直接染色2333
对于区间l[i]-r[i]进行染色,其实就是对该区间进行区间修改,将这个区间修改成i
到时候用桶的思路去记录整面墙上出现了几种颜色即可。
对了,为了防止某些左右端点都被遮住,只有中间露出来的小透明影响答案,可以再离散化之前把l+1,r-1也扔进去。
我并不知道这玩意到底正不正确,但是竟然A掉了

代码如下,如果有大佬能叉掉还请在评论区指正,注意这道题的本质只是为了向大家介绍线段树在遇上极大区间而实际使用的区间却没有这么多的时候可以使用离散化的思想。
离散化听着高大上但其实代码也就下面这么一点,不要慌张哦~
但是一定要学会啊,之后权值线段树和主席树都是要用的啊
#include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define lson root<<1 #define rson root<<1|1 using namespace std; struct node { int l,r,val,lazy; } tr[200020]; struct poster { int l,r; }p[40040]; int a[40040],cnt,ans[40040],cnt1[40040]; void push_down(int root) { tr[lson].val=tr[root].lazy; tr[rson].val=tr[root].lazy; tr[lson].lazy=tr[root].lazy; tr[rson].lazy=tr[root].lazy; tr[root].lazy=0; } void build(int root,int l,int r) { if(l==r) { tr[root].l=l; tr[root].r=r; tr[root].val=0; return ; } tr[root].l=l; tr[root].r=r; int mid=(tr[root].l+tr[root].r)>>1; build(lson,l,mid); build(rson,mid+1,r); } void update(int root,int l,int r,int val) { if(l==tr[root].l&&r==tr[root].r) { tr[root].val=val; tr[root].lazy=val; return ; } if(tr[root].lazy) { push_down(root); } int mid=(tr[root].l+tr[root].r)>>1; if(l>mid) { update(rson,l,r,val); } else { if(r<=mid) { update(lson,l,r,val); } else { update(lson,l,mid,val); update(rson,mid+1,r,val); } } } int query(int root,int pos) { if(pos==tr[root].l&&pos==tr[root].r) { return tr[root].val; } if(tr[root].lazy) { push_down(root); } int mid=(tr[root].l+tr[root].r)>>1; if(mid>=pos) { return query(lson,pos); } else { return query(rson,pos); } } int main() { int t,n; scanf("%d",&t); while(t--) { cnt=0; memset(cnt1,0,sizeof(cnt1)); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d %d",&p[i].l,&p[i].r); a[++cnt]=p[i].l; a[++cnt]=p[i].l+1; a[++cnt]=p[i].r; a[++cnt]=p[i].r-1; } sort(a+1,a+cnt+1); //由此开始离散化 cnt=unique(a+1,a+cnt+1)-a-1; for(int i=1;i<=n;i++) { p[i].l=lower_bound(a+1,a+cnt+1,p[i].l)-a; p[i].r=lower_bound(a+1,a+cnt+1,p[i].r)-a; //到这结束 } build(1,1,cnt); for(int i=1;i<=n;i++) { update(1,p[i].l,p[i].r,i); } for(int i=1;i<=cnt;i++) { ans[i]=query(1,i); } int num=0; for(int i=1;i<=cnt;i++) { if(cnt1[ans[i]]==0&&ans[i]!=0) { cnt1[ans[i]]=1; num++; } } printf("%d ",num); } }
既然连离散化都讲了,那不妨也来讲讲扫描线吧(什么神逻辑)
e.g.乱入 扫描线
扫描线这玩意一听就非常高级啊
它具体使用的范围是计算几何里,求矩形的面积并
来看一道例题吧
题意:给出平面上n个矩形的左下角坐标和右上角坐标,求平面被所有矩形覆盖的面积。
好吧,这玩意跟线段树有什么关系?
我感觉明显可以瞎搞啊
你瞧n<=200啊
但是如果可啪的出题人把数据范围造成了n<=100000呢(x,y的范围也极大)?

瞎搞不行了,我们考虑一下哪里能优化
一个矩形的面积可以表示为长乘宽,那么一个矩形能做出的贡献就是从第一条边出现一直到第二条边出现,在这中间与y轴平行的线段的长度是不变的。
有点蒙,那么来张图吧

所以想到了什么?
差分啊,差分啊,差分啊!
即使是几个矩形叠来叠去,在一条边出现到下一条边出现之间,与y轴平行的线段的长度也还是不变的。
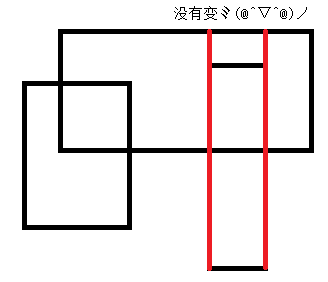
所以对于y轴上的长度,只有在遇到新的线段的时候才会变化,我们可以按照每条与y轴平行的边来分割矩形。
面积就是与y轴平行的当前长度和*(x[i]-x[i-1])
好的,那跟线段树有什么关系呢?
因为与y轴平行的长度和可以用线段树维护啊!
在第一条线段进入的时候对于y轴平行的那条线加入一条长度为ly[i]~ry[i]的线段
第二条线进入的时候删除这条线段,线段树维护长度和 ,这样子可以非常美妙的适应强制在线的非常大的数据。
如果理解了的话,这就变成了一道区间覆盖问题,支持插入一条线段,删除一条线段,求当前所有线段覆盖的长度
此时的线段树要稍微更改一下
从push_up到update都要改(烦躁ing)
push_up的改变应该很好看懂,如果这一段lazy大于0,说明区间被全覆盖,长度为区间长度,否则则是两个子树的长度之和
build建右子树的时候mid+1改成mid,建的树同时记录实数的nl-nr和伪离散化的l-r
update见代码,不是很好解释,反正不难。
当初学的时候大概膜了好几份代码,这份是最好看懂得,我把它魔改了一发,应该也比较接近平日里自己的写法。
代码如下:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define lson root<<1 #define rson root<<1|1 #define N 100010 using namespace std; struct line { double x,y1,y2; int val; } l[N]; bool cmp(line a,line b) { return a.x<b.x; } struct node { double nl,nr,len; int l,r,lazy; } tr[N<<2]; double a[N]; void push_up(int root) { if(tr[root].lazy>0) { tr[root].len=tr[root].nr-tr[root].nl; } else { if(tr[root].r-tr[root].l==1) { tr[root].len=0; } else { tr[root].len=tr[lson].len+tr[rson].len; } } } void build(int root,int l,int r) { if(l+1==r) { tr[root].l=l,tr[root].r=r; tr[root].nl=a[l],tr[root].nr=a[r]; tr[root].lazy=0,tr[root].len=0.0; return ; } tr[root].l=l,tr[root].r=r; tr[root].nl=a[l],tr[root].nr=a[r]; tr[root].lazy=0,tr[root].len=0.0; int mid=(l+r)>>1; build(lson,l,mid); build(rson,mid,r); } void update(int root,double l,double r,int val) { if(tr[root].nl==l&&tr[root].nr==r) { tr[root].lazy+=val; push_up(root); return ; } if(r<=tr[lson].nr) { update(lson,l,r,val); } else { if(l>=tr[rson].nl) { update(rson,l,r,val); } else { update(lson,l,tr[lson].nr,val); update(rson,tr[rson].nl,r,val); } } push_up(root); } int main() { int n,cnt,ttt=0; while(scanf("%d",&n)!=EOF&&n) { ttt++; cnt=0; double x1,x2,y1,y2; for(int i=1;i<=n;i++) { scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); l[++cnt].x=x1;l[cnt].y1=y1;l[cnt].y2=y2;l[cnt].val=1; a[cnt]=y1; l[++cnt].x=x2;l[cnt].y1=y1;l[cnt].y2=y2;l[cnt].val=-1; a[cnt]=y2; } sort(l+1,l+cnt+1,cmp); sort(a+1,a+cnt+1); build(1,1,cnt); update(1,l[1].y1,l[1].y2,l[1].val); double ans=0.0; for(int i=2;i<=cnt;i++) { ans+=tr[1].len*(l[i].x-l[i-1].x); update(1,l[i].y1,l[i].y2,l[i].val); } printf("Test case #%d ",ttt); printf("Total explored area: %.6lf ",ans); puts(""); } }
大体单标记的操作都有一些介绍了,更难的东西也是有的,但无外乎就是这个思想。
当然,除了单标记,还有双标记这种更加神奇的操作
e.g.5(线段树区间修改——双标记)
啊,你终于帮助老师写出了一颗带区间修改的线段树,结果老师眉头一皱,发现事情并不简单。
原来,这些考场考得是不一样的卷子,按照卷子的不同要乘上不同比例的权值。
简单地说,就是既要实现区间加又要实现区间乘,最后可怜的你还是要出求区间和2333
这个例题就足以引出双标记了,其实如果理解了单标记,双标记也就不是很难了
双标记之所以有别于单标记,就是因为标记还有先后顺序。
先后顺序,这似乎代表着一堆zz的分类讨论,但是不要慌,其实它并不复杂。
我们来考虑一下哪种计算先比较优越,
首先,是我们的一号选手,人类最古老的数学符号,数学殿堂中的长者——加♂法
算了,太中二了,反正我们就随便考虑一下先加后乘会咋样吧,比如说现在原数为a,加标记为b,乘标记为c
来来来,现在的值是(a+b)*c,好像没有什么问题呢~
呵呵,谁告诉你我们实际修改的时候一定是加标记在前的呢?
如果先乘再加呢?
(a+(b/c))*c
emmm,看,我的精度,他飞起来啦qwq
好的,那么先乘再加就一定有用了吗?
sorry,先乘再加是真的可以为所欲为的!
为什么呢?
因为乘标记再先乘后加是这样子的
a*c+b
先加后乘是这样子的
a*c+b*c
有没有发现,只需要在进行乘操作的时候把加标记乘上c就可以了。
反过来,加法也可以这么做,但是小心你的精度2333
还是照例来到例题
已知一个数列,你需要进行下面三种操作:
1.将某区间每一个数乘上x
2.将某区间每一个数加上x
3.求出某区间每一个数的和
代码写的时候注意开longlong 感谢hpw大佬的代码,对我很有启发
代码如下:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define ll long long #define lson root<<1 #define rson root<<1|1 #define N 400010 using namespace std; struct node { ll l,r,sum,add=0,mul=1; }tree[N]; int n,m,p; void push_up(int root) { tree[root].sum=(tree[lson].sum+tree[rson].sum)%p; } void push_down(int root) { int mid=(tree[root].l+tree[root].r)>>1; tree[lson].sum=(tree[lson].sum*tree[root].mul+tree[root].add*(mid-tree[root].l+1))%p; tree[rson].sum=(tree[rson].sum*tree[root].mul+tree[root].add*(tree[root].r-mid))%p; tree[lson].mul=(tree[lson].mul*tree[root].mul)%p; tree[rson].mul=(tree[rson].mul*tree[root].mul)%p; tree[lson].add=(tree[lson].add*tree[root].mul+tree[root].add)%p; tree[rson].add=(tree[rson].add*tree[root].mul+tree[root].add)%p; tree[root].add=0; tree[root].mul=1; return; } void build(int l,int r,int root) { if(l==r) { tree[root].l=l; tree[root].r=r; scanf("%lld",&tree[root].sum); return; } tree[root].l=l; tree[root].r=r; int mid=(l+r)>>1; build(l,mid,lson); build(mid+1,r,rson); push_up(root); return; } void add(int l,int r,int root,ll k) { if(l==tree[root].l&&r==tree[root].r) { tree[root].add=(tree[root].add+k)%p; tree[root].sum=(tree[root].sum+k*(tree[root].r-tree[root].l+1))%p; return ; } int mid=(tree[root].l+tree[root].r)>>1; push_down(root); if(r<=mid) { add(l,r,lson,k); } else { if(l>mid) { add(l,r,rson,k); } else { add(l,mid,lson,k); add(mid+1,r,rson,k); } } push_up(root); } void mul(int l,int r,int root,ll k) { if(l==tree[root].l&&r==tree[root].r) { tree[root].sum=(tree[root].sum*k)%p; tree[root].mul=(tree[root].mul*k)%p; tree[root].add=(tree[root].add*k)%p; return ; } int mid=(tree[root].l+tree[root].r)>>1; push_down(root); if (r<=mid) { mul(l,r,lson,k); } else { if (l>mid) { mul(l,r,rson,k); } else { mul (l,mid,lson,k); mul(mid+1,r,rson,k); } } push_up(root); } ll query (int l,int r,int root) { if(l==tree[root].l&&r==tree[root].r) { return tree[root].sum%p; } int mid=(tree[root].l+tree[root].r)>>1; push_down(root); if(r<=mid) { return query(l,r,lson); } else { if(l>mid) { return query(l,r,rson); } else { return (query(l,mid,lson)+query(mid+1,r,rson))%p; } } } int main () { scanf("%d%d%d",&n,&m,&p); build(1,n,1); for(int i=1; i<=m; ++i) { int oper; scanf("%d",&oper); if(oper==1) { int l,r; ll k; scanf("%d%d%lld",&l,&r,&k); mul(l,r,1,k); } else { if(oper==2) { int l,r; ll k; scanf("%d%d%lld",&l,&r,&k); add(l,r,1,k); } else { int l,r; scanf("%d%d",&l,&r); printf("%lld ",query(l,r,1)%p); } } } return 0; }
e.g.6(zkw线段树点修改)
好了现在毒瘤的老师(出题人)已经不满足于100000的数据了,他魔改了时限和数据范围,几乎卡到了nlogn的极限,然后还是询问区间最大值。
你觉得你的线段树常数优越,随手一交就又一次完成了任务,但是你的菜鸡同学xhk TLE了(话说这不是给我的任务吗?为什么xhk会来掺和一脚啊,好气啊!)
秉着同窗的情谊,你开始教他zkw线段树
zkw线段树又被称为非递归版线段树,常数比普通线段树要小很多,这是因为zkw线段树用的几乎都是for循环,这省去了很多时间和空间。
因为c++的递归用的是栈机制,额外的空间复杂度与递归次数呈线性比例,同时,因为调用了大量函数,时间开销也会变大。
之所以需要普通线段树要用递归写,是因为递归好理解。
但其实非递归的线段树也不是非常难理解,非常难写。相反,它很短很精悍。
所以zkw神犇提出了它,并说明了它的几个优点:
常数小,空间小,代码短
那简直是太优了!所以zkw线段树应该怎么实现呢?
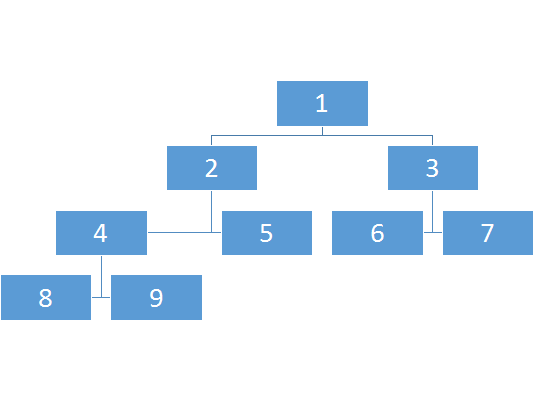
让我们重新来看一看线段树的构造吧!
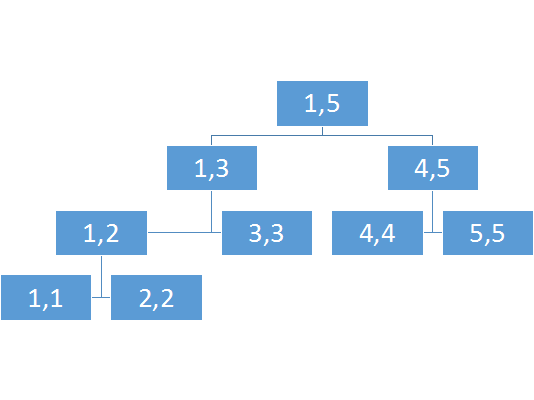
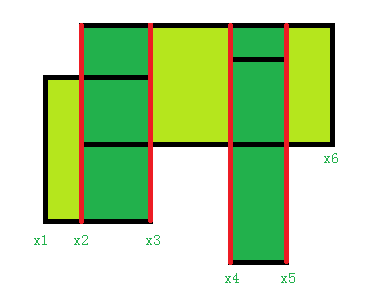
按照我们存图的编号来说它会是这样的:
因为我们不用递归,所以建树时需要用一个科学的方法找到叶子节点,那么这种树合适吗?显然是不合适的,因为叶子结点没有连续性。上面可能还看不出来,这个就很明显了。
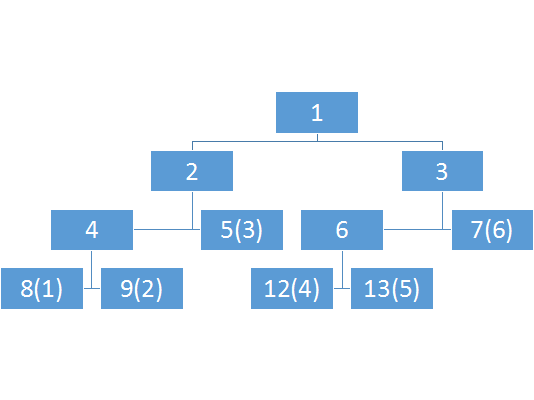
其中点1-6分别对应8、9、5、12、13、7
完全没有任何简单规律。
所以树的结构要改一下,改成什么呢?
还记得最初那颗不科学的线段树吗?

这棵树的叶子结点是连续的 ,但是它只能支持2的幂次的建树。
为什么呢?因为底层的叶子节点数不够多(一本正经的胡说八道)
那么就给它足够多的叶子结点啊(何不食肉糜式的回答233)
但是这真不难,你只需要先建一颗足够大的满二叉树,然后把那一个数组挂上去就行了。
有多大呢?自然是底层的满叶子结点个数大于数组的大小。
即满叶子结点个数为第一个大于n+1的2的幂次。
然后再把n全部挂上去。
是的,这看起来是比普通线段树耗内存,但其实也没超过四倍的内存,还是可以接受的(顺便一提,他的空间复杂度还是比一般线段树优越)。
而且,我们可以直接获得这些要读入的叶子结点的位置。
接着我们倒着一层一层往上推(因为一个点的编号必定大于它的父节点,我们可以直接for i=bit;i>0;i--)
不过要注意,我们不挂第一个叶子节点(为什么先自己想想)
于是建树就写出来了!
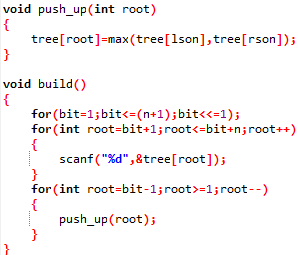
那么点修改呢?
是的,因为知道了叶子结点的位置,我们可以很轻松地直接修改叶子结点,然后从下往上推父节点,这代码,清真!

但是查询略微有一点难理解
先举个栗子吧,如果我现在建了这么一棵有6个节点的zkw线段树,我要查询1-6的最小值,那么我需要的是哪几块?
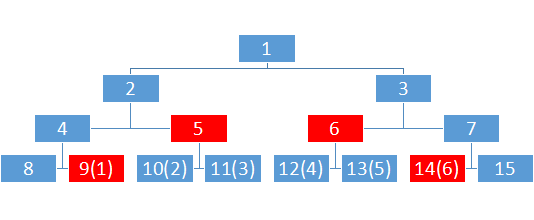
没错,是图中的9,5,6,14
诶,那么每次先把l和r扔到底层然后一层一层往上跳,如果l是奇数就统计答案,r是偶数就统计答案,岂不美哉?
naive!
来来来,再看看上面这张图
11的上面是5,,恭喜你,顺便把2也算进去了
所以我们现在需要一种查询
能够完成logn的查询区间最大值,而且不会错误的将不属于该区间的块记录进来
感觉很难搞吧,其实还真有一种可以胜任此工作的查询方法,原理和上面的差不多
我们在底层将l指向l-1,r指向r+1,像这张图一样跳上来
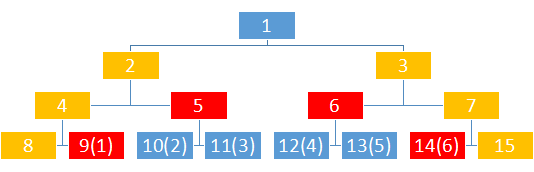
你发现了什么?
什么也没发现????
好吧,是在下输了,我再来张图,现在是查询3-5
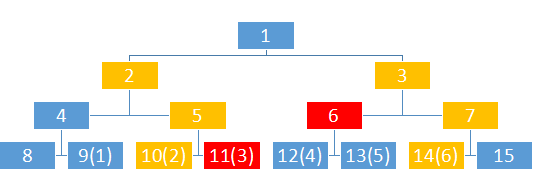
这似乎是非常明显了,如果l是偶数,就加上他的右兄弟(父亲节点的右子树),如果r是奇数,就加上他的左兄弟(父亲节点的左子树)
结束的条件是l==r-1
这可以保证查询到的区间一定是我们想要的,因为这些区间的范围肯定在(l-1,r+1)之内,被l和r限制着,STO zkw神犇
好的,所以可以非常轻松地发现,这种查询查询的是开区间。
这也就是我们之前为什么不挂地一个叶子节点的原因。
为了方便查询开区间(0,n+1)的值,很显然我们不会遇上n是上面15节点之类的情况,具体为什么请回顾建树的过程
好的,查询代码如下:

现在zkw线段树所有需要用的代码都写完了,来个总代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define lson root<<1 #define rson root<<1|1 int n,m,bit; char c; int tree[800080]; void push_up(int root) { tree[root]=max(tree[lson],tree[rson]); } void build() { for(bit=1; bit<=(n+1); bit<<=1); for(int root=bit+1; root<=bit+n; root++) { scanf("%d",&tree[root]); } for(int root=bit-1; root>=1; root--) { push_up(root); } } void update(int root,int v) { for(tree[root+=bit]=v,root>>=1; root>0; root>>=1) { push_up(root); } } int query(int l,int r) { int ans=0; for(l+=bit-1,r+=bit+1; l^r^1; l>>=1,r>>=1) { if(~l&1) { ans=max(ans,tree[l^1]); } if(r&1) { ans=max(ans,tree[r^1]); } } return ans; } int main() { while(scanf("%d%d",&n,&m)!=EOF) { build(); for(int i=1; i<=m; i++) { int a,b; scanf(" %c%d%d",&c,&a,&b); if(c=='Q') { printf("%d ",query(a,b)); } else { update(a,b); } } } }
zkw线段树单点修改区间求和也是好写的, 以hdu1166为例
代码如下:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define lson root<<1 #define rson root<<1|1 int n,m,bit; char c[10]; int tree[800080]; void push_up(int root) { tree[root]=tree[lson]+tree[rson]; } void build() { for(bit=1; bit<=(n+1); bit<<=1); for(int root=bit+1; root<=bit+n; root++) { scanf("%d",&tree[root]); } for(int root=bit-1; root>=1; root--) { push_up(root); } } void update(int root,int v) { for(tree[root+=bit]+=v,root>>=1; root>0; root>>=1) { push_up(root); } } int query(int l,int r) { int ans=0; for(l+=bit-1,r+=bit+1; l^r^1; l>>=1,r>>=1) { if(~l&1) { ans+=tree[l^1]; } if(r&1) { ans+=tree[r^1]; } } return ans; } int main() { int t,ttt=0; scanf("%d",&t); while(t--) { ttt++; printf("Case %d: ",ttt); memset(tree,0,sizeof(tree)); scanf("%d",&n); build(); for(; 1; ) { int a,b; scanf(" %s",&c); if(c[0]=='E') { break; } scanf("%d %d",&a,&b); if(c[0]=='Q') { printf("%d ",query(a,b)); } else { if(c[0]=='A') { update(a,b); } else { if(c[0]=='S') { update(a,-b); } } } } } }
至于区间修改,你会发现因为zkw是从下到上查询的所以标记什么的就gg了,但是zkw神犇提出了差分的做法,说句实话感觉不明觉厉,所以区间修改还是乖乖地写普通线段树吧~(之所以不再写下去的原因是因为没(zuo)有(zhe)必(hen)要(lan)了)
自带大常数的xhk你还是爆零吧~
至于zkw线段树有多优越,看看下面这两张图就知道了~感谢xhk提供的大常数普通线段树~



说起来普通线段树,老师灵机一动又改了需求
e.g.7(权值线段树求第k小,rank,前驱后继)
嗯,老师终于不来找你改分数了,他来询问你一个新的毒瘤问题
他会有六种操作
第一种:给你一个同学的成绩
第二种:让你删掉一个同学的成绩
第三种:询问这些成绩中第k小的是哪个
第四种:询问某同学的得分x在这些成绩中排第几
第五种:找到比该同学高的最低分数
第六种:找到比该同学低的最高分数
总操作数为100000
你嘿嘿一笑:“来,老师,splay、treap拿去不谢,不满意我这还有红黑树。”
老师眉头一皱:“我觉得你之前那个算法挺好的,你就用那个来实现一下吧。”
好的,你开始写权值线段树。
如果我们不再按照区间建树而是改去按照每个数出现的次数建树会怎么样?
比如说1,1,2,4,5这个序列,线段树建成这个样子,维护的是区间和
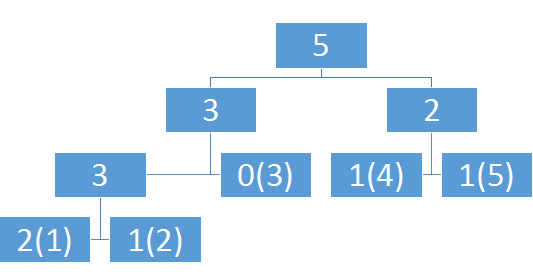
那么这有什么用呢?
我们来分析一下这几个问题的具体意思
第一个第二个是插入和删除,就不需要分析了,pass,下一个!
第三个是查询第k小数
如果某个数之前(包括自己)有k个数以上,且这个数之前(不包括自己)的数的个数不到k个,那么这个数就是第k小
第四个是求某数的排名
这就是这个数之前数的个数加一
第五第六个前驱和后继就是这个数之前(之后)第一个出现的数,也就是个数大于等于一的最近的一个数,可以二分区间啦~
所以我们只要有一个能够logn计算有多少个数比他小的数据结构就可以啦,是什么呢?
权值线段树啊
在上面那张图里,你可以通过query 1~x来求出x之前有多少个数啦~
所以这些问题就都迎刃而解了,可以实现每个操作log^2 n以内。
现在来道例题
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入xx 数
- 删除xx 数(若有多个相同的数,因只删除一个)
- 查询xx 数的排名(排名定义为比当前数小的数的个数+1+1 。若有多个相同的数,因输出最小的排名)
- 查询排名为xx 的数
- 求xx 的前驱(前驱定义为小于xx ,且最大的数)
- 求xx 的后继(后继定义为大于xx ,且最小的数)
额,看着很简单?来,把数据范围供上来!

emmm,n还是可以接受的,但是值域……太大了啊!
怕什么?我们有离散化。
kth和排名都可以logn搞,前驱后继我瞎胡了一种log^2 n的做法,如果有大佬能够给出logn的做法还请不吝赐教~
代码如下:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define lson root<<1 #define rson root<<1|1 using namespace std; struct node { int l,r,sum; } tr[800080]; struct opt { int kd,x; } op[100010]; int cnt,a[100010]; void push_up(int root) { tr[root].sum=tr[lson].sum+tr[rson].sum; } void build(int root,int l,int r) { if(l==r) { tr[root].l=l; tr[root].r=r; tr[root].sum=0; return ; } tr[root].l=l; tr[root].r=r; int mid=(l+r)>>1; build(lson,l,mid); build(rson,mid+1,r); push_up(root); } void update(int root,int pos,int val) { if(tr[root].l==pos&&tr[root].r==pos) { tr[root].sum+=val; return ; } int mid=(tr[root].l+tr[root].r)>>1; if(mid>=pos) { update(lson,pos,val); } else { update(rson,pos,val); } push_up(root); } int query(int root,int l,int r) { if(l>r) { return 0; } if(tr[root].l==l&&tr[root].r==r) { return tr[root].sum; } int mid=(tr[root].l+tr[root].r)>>1; if(mid<l) { return query(rson,l,r); } else { if(r<=mid) { return query(lson,l,r); } else { return query(lson,l,mid)+query(rson,mid+1,r); } } } int kth(int root,int k) { if(tr[root].l==tr[root].r) { return tr[root].l; } if(tr[lson].sum>=k) { return kth(lson,k); } else { return kth(rson,k-tr[lson].sum); } } int rank(int x) { int pos=lower_bound(a+1,a+cnt+1,x)-a; return query(1,1,pos-1)+1; } int pre(int root,int pos) { int l=1,r=pos-1,mid; while(l<r) { mid=(l+r)>>1; if(query(1,mid+1,r)) { l=mid+1; } else { r=mid; } } return r; } int next(int root,int pos) { int l=pos+1,r=cnt,mid; while(l<r) { mid=(l+r)>>1; if(query(1,l,mid)) { r=mid; } else { l=mid+1; } } return l; } int main() { int n; scanf("%d",&n); for(int i=1; i<=n; i++) { scanf("%d%d",&op[i].kd,&op[i].x); if(op[i].kd!=2&&op[i].kd!=4) { a[++cnt]=op[i].x; } } sort(a+1,a+cnt+1); cnt=unique(a+1,a+cnt+1)-a-1; build(1,1,cnt); for(int i=1; i<=n; i++) { if(op[i].kd==1) { int pos=lower_bound(a+1,a+cnt+1,op[i].x)-a; update(1,pos,1); } if(op[i].kd==2) { int pos=lower_bound(a+1,a+cnt+1,op[i].x)-a; update(1,pos,-1); } if(op[i].kd==3) { printf("%d ",rank(op[i].x)); } if(op[i].kd==4) { int pos=kth(1,op[i].x); printf("%d ",a[pos]); } if(op[i].kd==5) { int pos=lower_bound(a+1,a+cnt+1,op[i].x)-a; printf("%d ",a[pre(1,pos)]); } if(op[i].kd==6) { int pos=lower_bound(a+1,a+cnt+1,op[i].x)-a; printf("%d ",a[next(1,pos)]); } } }
好的,终于到主席树了(松气)
e.g.8(主席树求区间第k小)
毒瘤老师又一次提出了非分的要求,他希望查找所有考试成绩中你们班的倒数第k名,即一段连续区间的第k小(为什么一个班在同一个考场考呢,这是一个值得深思的问题)
区间第k小啊,这不是很好办呢。
反正求第k小的话,权值线段树的思路是可以借鉴的,然后我们想想如果对于区间l~r的第k大,我们已经知道了1~l-1的权值线段树,又知道了1~r的权值线段树,那么根据前缀和的思路,我们可以很轻松的求出l~r的权值线段树,对于这棵树进行求区间第k大即可
但是首先建n棵线段树就已经不是我们能够接受的了
复杂度实在太高,肯定不能适应100000的数据范围,同时,空间也是硬伤
那么怎么办呢?
我们分析一下,每次主席树的操作,是不是所有的点都会变呢?
如果不会的话我们自然可以有多少个变就改多少个了。
很幸运,与update的复杂度一样,每次插入新的数字只会改变logn个节点,那么我们新建这logn个节点就可以了。(这玩意应该不用解释为什么吧,因为update就只会遍历logn次)
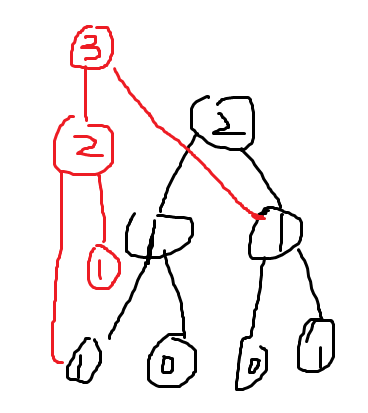
对于每个节点记录他的左子树右子树编号,这个编号不再由root<<1,root<<1|1推得,而是由数组l和r记录。
如果哪个子树不再被影响,那么就把他的原来的子树接上来。
主席树就是这个思路啦
查询的时候就查插入第l-1个数到插入第r个数的差的树的第k小就可以了
具体的操作就看看代码吧
照例来到例题:
题意就是求区间第k小
那么就是最裸的主席树。
代码如下:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define mid ((l+r)>>1) #define hi puts("hi"); using namespace std; #define N 200010 int n,m,q,cnt=0; int a[N],b[N],T[N]; int sum[N<<5],L[N<<5],R[N<<5]; int build(int l,int r) { int rt=++cnt; sum[rt]=0; if(l<r) { L[rt]=build(l,mid); R[rt]=build(mid+1,r); } return rt; } int update(int pre,int l,int r,int x) { int rt=++cnt; L[rt]=L[pre]; R[rt]=R[pre]; sum[rt]=sum[pre]+1; if(l<r) { if(x<=mid) { L[rt]=update(L[pre],l,mid,x); } else { R[rt]=update(R[pre],mid+1,r,x); } } return rt; } int query(int u,int v,int l,int r,int k) { if(l>=r) { return l; } int x=sum[L[v]]-sum[L[u]]; if(x>=k) { return query(L[u],L[v],l,mid,k); } else { return query(R[u],R[v],mid+1,r,k-x); } } int main() { scanf("%d%d",&n,&q); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); b[i]=a[i]; } sort(b+1,b+n+1); m=unique(b+1,b+1+n)-b-1; T[0]=build(1,m); for(int i=1;i<=n;i++) { int t=lower_bound(b+1,b+1+m,a[i])-b; T[i]=update(T[i-1],1,m,t); } while(q--) { int ll,rr,kk; scanf("%d%d%d",&ll,&rr,&kk); int t=query(T[ll-1],T[rr],1,m,kk); printf("%d ",b[t]); } return 0; }
啊,写了三天终于写完了,本来当初的flag还有二维线段树和树状数组的,结果是在写不动了orz
平均一天3000字(不含制图)真的快要赶上网文作家了,代码写到死啊,不过还是很有成就感的
嗯,就这样了