LibreOJ 6281 数列分块入门 5(分块区间开方区间求和)

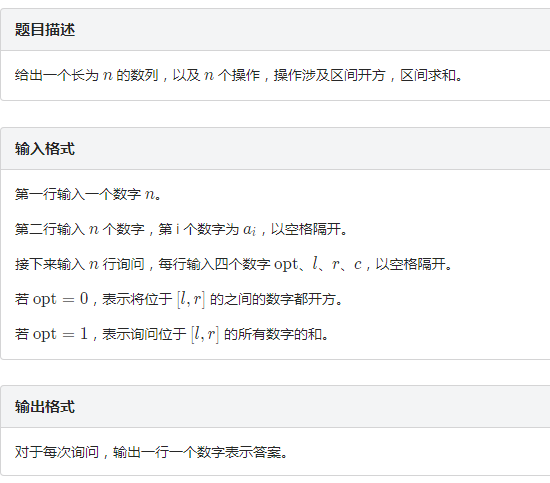
题解:区间开方emmm,这马上让我想起了当时写线段树的时候,很显然,对于一个在2^31次方以内的数,开方7-8次就差不多变成一了,所以我们对于每次开方,如果块中的所有数都为一了,那么开方也没有必要了.

所以开个tag标记一下当前块是否均为一,如果不是的话每次暴力构块即可

代码如下:

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

long long a[100010],tag[100010],sum[100010],lump[100010];
int n,sz;

void reset(int x)
{
    if(tag[x])
    {
        return;
    }
    sum[x]=0;
    tag[x]=1;
    for(int i=(x-1)*sz+1;i<=min(sz*x,n);i++)
    {
        a[i]=sqrt(a[i]);
        sum[x]+=a[i];
        if(a[i]>1)
        {
            tag[x]=0;
        }
    }
}

void add(long long l,long long r)
{
    for(int i=l;i<=min(sz*lump[l],r);i++)
    {
        sum[lump[i]]-=a[i];     //lump!!!
        a[i]=sqrt(a[i]);
        sum[lump[i]]+=a[i];
    }
    if(lump[l]!=lump[r])
    {
        for(int i=(lump[r]-1)*sz+1;i<=r;i++)
        {
            sum[lump[i]]-=a[i];
            a[i]=sqrt(a[i]);
            sum[lump[i]]+=a[i];
        }
    }
    for(int i=lump[l]+1;i<=lump[r]-1;i++)
    {
        reset(i);
    }
}

long long query(long long l,long long r)
{
    long long ans=0;
    for(int i=l;i<=min(lump[l]*sz,r);i++)
    {
        ans+=a[i];
    }
    if(lump[l]!=lump[r])
    {
        for(int i=(lump[r]-1)*sz+1;i<=r;i++)
        {
            ans+=a[i];
        }
    }
    for(int i=lump[l]+1;i<=lump[r]-1;i++)
    {
        ans+=sum[i];
    }
    return ans;
}

int main()
{
    long long opt,l,r,c;
    scanf("%d",&n);
    sz=sqrt(n);
    for(int i=1;i<=n;i++)
    {
        lump[i]=(i-1)/sz+1;
        scanf("%lld",&a[i]);
    }
    for(int i=1;i<=n;i++)
    {
        sum[lump[i]]+=a[i];
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%lld%lld%lld%lld",&opt,&l,&r,&c);
        if(!opt)
        {
            add(l,r);
        }
        else
        {
            printf("%lld
",query(l,r));
        }
    }
}