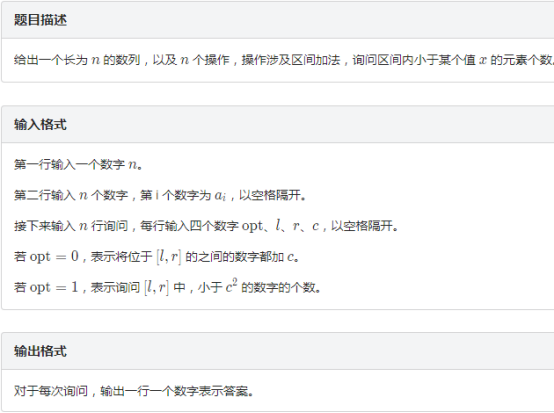

题解:非常高妙的分块,每个块对应一个桶,桶内元素全部sort过,加值时,对于零散块O(sqrt(n))暴力修改,然后暴力重构桶.对于大块直接整块加.查询时对于非完整块O(sqrt(n))暴力遍历.对于完整的大块用lower_bound或者手写二分log(sqrt(n)查找,总复杂度O(n*sqrt(n)*log(sqrt(n)))
代码如下:
#include<cmath> #include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int a[50010],lump[50010],tag[50010]; int n,sz; vector<int> v[1000]; void reset(int x) { v[x].clear(); for(int i=(x-1)*sz+1;i<=min(x*sz,n);i++) { v[x].push_back(a[i]); } sort(v[x].begin(),v[x].end()); } void add(int l,int r,int c) { for(int i=l;i<=min(lump[l]*sz,r);i++) { a[i]+=c; } reset(lump[l]); if(lump[l]!=lump[r]) { for(int i=(lump[r]-1)*sz+1;i<=r;i++) { a[i]+=c; } reset(lump[r]); } for(int i=lump[l]+1;i<=lump[r]-1;i++) { tag[i]+=c; } } int query(int l,int r,int c) { int ans=0; for(int i=l;i<=min(lump[l]*sz,r);i++) { if(a[i]+tag[lump[l]]<c) { ans++; } } if(lump[l]!=lump[r]) { for(int i=(lump[r]-1)*sz+1;i<=r;i++) { if(a[i]+tag[lump[r]]<c) { ans++; } } } for(int i=lump[l]+1;i<=lump[r]-1;i++) { int z=c-tag[i]; ans+=lower_bound(v[i].begin(),v[i].end(),z)-v[i].begin(); } return ans; } int main() { int opt,l,r,c; scanf("%d",&n); sz=sqrt(n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } for(int i=1;i<=n;i++) { lump[i]=(i-1)/sz+1; v[lump[i]].push_back(a[i]); } for(int i=1;i<=lump[n];i++) { sort(v[i].begin(),v[i].end()); } for(int i=1;i<=n;i++) { scanf("%d%d%d%d",&opt,&l,&r,&c); if(!opt) { add(l,r,c); } else { printf("%d ",query(l,r,c*c)); } } }