好吧,这名字真是让我想起了某段被某教科书支配的历史.....各种DP题层出不穷,不过终于做完了orz
虽然各种手糊加乱搞,但还是要总结一下.
T1 Monkey Banana Problem
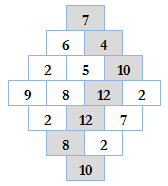
这道题和数塔问题差不多,不过多了一个倒过来的

代码如下:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; long long a[201][101],t,n; int main() { int ttt=0; scanf("%lld",&t); while(t--) { ttt++; memset(a,0,sizeof(a)); scanf("%lld",&n); for(int i=1; i<=n; i++) { for(int j=1; j<=i; j++) { scanf("%lld",&a[i][j]); } } for(int i=n+1; i<=2*n-1; i++) { for(int j=1; j<=2*n-i; j++) { scanf("%lld",&a[i][j]); } } for(int i=2; i<=n; i++) { for (int j=1; j<=i; j++) { a[i][j]+=max(a[i-1][j-1],a[i-1][j]); } } for(int i=n+1; i<=2*n-1; i++) { for(int j=1; j<=2*n-i; j++) { a[i][j]+=max(a[i-1][j],a[i-1][j+1]); } } printf("Case %d: %lld ",ttt,a[2*n-1][1]); } }
T2Rooks
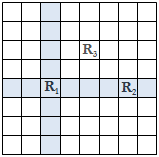

T3Marriage Ceremonies
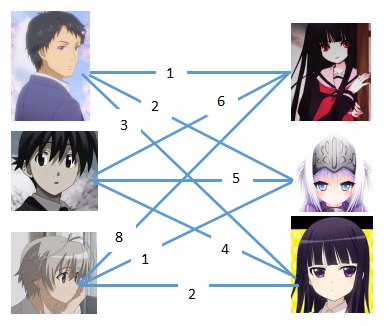
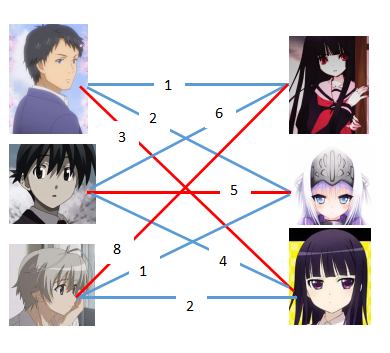

代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 17 int dp[N][1<<N]; int a[N][N]; int t,n,ans; int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; memset(dp,0,sizeof(dp)); memset(a,0,sizeof(a)); scanf("%d",&n); for(int i=0; i<n; i++) { for(int j=0; j<n; j++) { scanf("%d",&a[i][j]); } } for(int i=0; i<n; i++) { dp[0][(1<<i)]=a[0][i]; } for(int i=1; i<n; i++) { for(int sta=0; sta<=(1<<n)-1; sta++) { if(!dp[i-1][sta]) { continue; } for(int j=0; j<n; j++) { if(sta&(1<<j)) { continue; } dp[i][sta|(1<<j)]=max(dp[i][sta|(1<<j)],dp[i-1][sta]+a[i][j]); } } } printf("Case %d: %d ",ttt,dp[n-1][(1<<n)-1]); } }
T4Guilty Prince

代码:
#include<queue> #include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; char maze[30][30]; bool vis[30][30]; int t,n,m,ans,x,y; int bfs(int x,int y) { queue<pair<int,int> > q; q.push(make_pair(x,y)); vis[x][y]=1; while(!q.empty()) { int nx=q.front().first; int ny=q.front().second; q.pop(); if(!vis[nx+1][ny]&&nx+1<=n&&nx+1>=1&&ny<=m&&ny>=1) { q.push(make_pair(nx+1,ny)); ans++; vis[nx+1][ny]=1; } if(!vis[nx-1][ny]&&nx-1<=n&&nx-1>=1&&ny<=m&&ny>=1) { q.push(make_pair(nx-1,ny)); ans++; vis[nx-1][ny]=1; } if(!vis[nx][ny+1]&&nx<=n&&nx>=1&&ny+1<=m&&ny+1>=1) { q.push(make_pair(nx,ny+1)); ans++; vis[nx][ny+1]=1; } if(!vis[nx][ny-1]&&nx<=n&&nx>=1&&ny-1<=m&&ny-1>=1) { q.push(make_pair(nx,ny-1)); ans++; vis[nx][ny-1]=1; } } } int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; ans=1; scanf("%d%d",&m,&n); memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { cin>>maze[i][j]; if(maze[i][j]=='@') { x=i; y=j; } if(maze[i][j]=='#') { vis[i][j]=1; } } } bfs(x,y); printf("Case %d: %d ",ttt,ans); } }
T5 Brush (III)

给你一个刷子,刷子有宽度w,允许你平行x轴刷k次,告诉你有n个点,求刷k次能刷完的最多的点的个数.
好吧,最初就是想暴力乱搞,然后发现xi,yi都有10^9,就想到了离散化.离散化y的坐标,统计一个cnt[i]表示第i个y值上有几个点,然后再搞一个num[i]表示以y[i]为下界宽为w的区域中点的个数,不过因为cnt数组足以胜任这一点。
然后就可以开始dp了
对于每一个cnt[i],我们可以选择从这个点开始刷还是不刷,对于每个点来说往左刷一个单位还是往右刷一个单位显然是没有任何意义的,即我们还是得从以每个点开始dp
很容易推出dp的转移方程
dp[i][j]表示刷到第j个点以后已经刷了i次的最大值
那么dp[i][j]=max{dp[i][j],dp[i-1][( 1~( j-1))]+cnt[j]}
代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 110 struct point { int x,y; } poi[N]; int n,w,k,t,tmp,ans; int cnt[N],y[N],dp[N][N]; bool cmp(point a,point b) { return a.y<b.y; } void discretization_it() { sort(poi+1,poi+n+1,cmp); tmp=1; y[tmp]=poi[1].y; cnt[tmp]=1; for(int i=2; i<=n; i++) { if(poi[i].y==y[tmp]) { cnt[tmp]++; } else { y[++tmp]=poi[i].y; cnt[tmp]=1; } } for(int i=1; i<=tmp; i++) { for(int j=i+1; j<=tmp; j++) { if(y[j]-y[i]<=w) { cnt[i]+=cnt[j]; } } } } int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; ans=0; memset(dp,0,sizeof(dp)); scanf("%d%d%d",&n,&w,&k); for(int i=1; i<=n; i++) { scanf("%d %d",&poi[i].x,&poi[i].y); } discretization_it(); for(int i=1; i<=tmp; i++) { dp[1][i]=cnt[i]; } for(int i=2; i<=k;i++) { for(int j=1; j<=tmp; j++) { for(int l=1; l<j; l++) { if (y[j]-y[l]<=w) { break; } if (y[j]-y[l]>w&&dp[i][j]<dp[i-1][l]+cnt[j]) { dp[i][j]=dp[i-1][l]+cnt[j]; } } } } for(int i=1;i<=k;i++) { for(int j=1;j<=tmp;j++) { ans=max(ans,dp[i][j]); } } printf("Case %d: %d ",ttt,ans); } }
T6 Brush (IV)
这回的刷子升级了,可以向任意的方向刷,不过刷子没有宽度,即几个点共线才能被刷掉,求刷掉所有点的最小次数
因为点的个数的数据范围只有16,所以可以想到状态压缩动态规划,选取i,j两个点,无非是选择是否要连i,j然后如果要选的话就把和i,j三点共线的所有点都加到当前的状态里去,然后花费1的次数将之前状态转移到现在状态。假设a[i][j]为i,j所在直线上的点的个数,这里a[i][j]表示二进制位下在i,j直线上所有点的位置。
所以dp[sta|a[i][j]]=min{dp[sta|a[i][j],dp[sta]+1}
代码:
#include<cstdio> #include<vector> #include<string> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define inf 0x3f3f3f3f struct point { int x,y; }poi[20]; int a[20][20]; int dp[(1<<17)]; int n,t; vector <int> yyk[(1<<17)]; //int lowbit(int x) //{ // return x&-x; //} bool judge(point x,point y,point z) { int tmp=(y.x-x.x)*(z.y-x.y)-(y.y-x.y)*(z.x-x.x); if(!tmp) { return 1; } else { return 0; } } void pre() { memset(a,0,sizeof(a)); for(int i=0;i<n;i++) { a[i][i]|=(1<<i); for(int j=i+1;j<n;j++) { for(int k=0;k<n;k++) { if(judge(poi[i],poi[j],poi[k])) { a[i][j]|=(1<<k); } } } } } void db() { for(int sta=0;sta<=(1<<16);sta++) { for(int j=0;j<16;j++) { if((sta&1<<j)==0) { yyk[sta].push_back(j); } } } } int main() { int ttt=0; scanf("%d",&t); db(); while(t--) { ttt++; scanf("%d",&n); for(int i=0;i<=(1<<n);i++) { dp[i]=inf; } for(int i=0;i<n;i++) { scanf("%d %d",&poi[i].x,&poi[i].y); } pre(); dp[0]=0; for(int sta=0;sta<(1<<n)-1;sta++) { int x=yyk[sta][0]; for(int j=0;j<yyk[sta].size();j++) { int y=yyk[sta][j]; dp[sta|a[x][y]]=min(dp[sta|a[x][y]],dp[sta]+1); } } printf("Case %d: %d ",ttt,dp[(1<<n)-1]); } return 0; }
T7 Painful Bases
给出一个值base,一个值k,一个base进制下的的数,求该数的全排列中模k余0的数的个数。
emmmm。。。这倒是比较老的套路了。。。首先看到求模数为几,自然是想到开一维来记录模数,这有点类似于数位dp中某些题的思路。而再乍一看这个给的数的长度不会超过16,自然是想到用状压去做。所以设置dp[sta][mod]表示当已经放好sta个数后这些数余数为mod的数的个数。
所以状态转移方程如下:dp[sta|(1<<j)][(mod*base+a[j]%k)%k]+=dp[sta][mod]
代码:
#include<cstdio> #include<string> #include<cstring> #include<iostream> #include<algorithm> using namespace std; long long dp[30][(1<<17)]; char s[20]; int t,base,k,a[20]; int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; memset(dp,0,sizeof(dp)); scanf("%d%d",&base,&k); cin>>s; int len=strlen(s); for(int i=0;i<len;i++) { if(s[i]<='9'&&s[i]>='0') { a[i]=s[i]-'0'; } else { a[i]=s[i]-'A'+10; } } int up=1<<len; dp[0][0]=1; for(int sta=0;sta<up;sta++) { for(int j=0;j<len;j++) { if(sta&(1<<j)) { continue; } for(int x=0;x<k;x++) { if(!dp[x][sta]) { continue; } dp[(x*base+a[j])%k][sta|(1<<j)]+=dp[x][sta]; } } } printf("Case %d: %lld ",ttt,dp[0][up-1]); } }
T8 the specials menu
给出一个字符串,求这个字符串中回文串的个数,你可以去掉一些字母。
噫,又是套路。。。区间dp老题了
用dp[i][j]表示区间i-j之间的方案数
则存在以下两种转移
1.s[i]=s[j]时:只留ij显然多了一种方案,dp[i][j]=dp[i+1][j]+dp[i][j-1]+1
2.s[i]!=s[j]时:显然存在重复dp[i][j]=dp[i+1][j]+dp[i][j-1]-dp[i+1][j-1]
代码:
#include<cstdio> #include<string> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 110 long long dp[N][N],t,ttt; int main() { scanf("%lld",&t); while(t--) { char s[N]; ttt++; memset(dp,0,sizeof(dp)); cin>>s+1; int len=strlen(s+1); for(int i=1;i<=len;i++) { dp[i][i]=1; } for(int i=len;i>=1;i--) { for(int j=i+1;j<=len;j++) { dp[i][j]+=dp[i+1][j]+dp[i][j-1]-dp[i+1][j-1]; if(s[i]==s[j]) { dp[i][j]+=dp[i+1][j-1]+1; } } } printf("Case %lld: %lld ",ttt,dp[1][len]); } }
T9 A Dangerous Maze
有n扇门,每扇门对应着一个值(xi),为正代表xi分后这个人能够离开,为负表示abs(xi)分后这个人会重新回到原地,并且这个人仍是1/n的概率重新再选一扇门。求他离开的期望?
好吧。。。感觉这道题又和dp没关系啊。。。
这是一道纯种的期望题。
首先对于门只有两种功能:要么把人传回去,要么送他出来,假设期望为E。当前耗时为C
这扇门是好门,将你传送出去,期望为C*1/n
这扇门是坏门,将你传送回来,期望为(E+C)*1/n
设总共有X扇坏门,好门消耗时间总和为sum1,坏门为sum2
则可以列出方程:
E=(sum1)/n+(E*X+sum2)/n
E=(sum1+sum2+E*X)/n
nE=sum1+sum2+E*X
(n-X)*E=sum1+sum2;
E=(sum1+sum2)/(n-X)
当然n-X为零的话他就永远出不去了
然而与dp并无关系的说。。。
代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int t,n,a,sum,div1,nag,pos; int gcd(int a,int b) { if(a%b==0) { return b; } return gcd(b,a%b); } int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; nag=0; sum=0; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a); if(a<0) { nag++; sum-=a; } else { sum+=a; } } pos=n-nag; if(pos==0) { printf("Case %d: inf ",ttt); } else { printf("Case %d: %d/%d ",ttt,sum/gcd(pos,sum),pos/gcd(pos,sum)); } } return 0; }
T10 Discovering Gold
已知有一个宽为1,长为n的表格,表格由1*1的小正方形组成,每个小正方形中都有一个价值v[i],现在从起点1开始掷骰子,掷到几就向前走几步,并获得当前走到位置的值v,
如果投过n就重投。求获得价值的期望。
著名oi选手xxx曾说过“一切期望皆方程”
好的这又不是一道dp题(大雾)
总而言之,著名oi选手xxx说过“概率正推,期望倒推”
所以DP[I]=(DP[I+1]+DP[I+2]+DP[I+3]+DP[I+4]+DP[I+5]+E[DP+6])/6+V[I]
代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 110 int a[N]; int n,t; double dp[N]; int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; scanf("%d",&n); memset(dp,0,sizeof(dp)); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } dp[n]=a[n]; for(int i=n-1;i>=1;i--) { int up; dp[i]=a[i]; if(n-i<6) { up=n-i; } else { up=6; } for(int j=1;j<=up;j++) { dp[i]+=(1.0/up)*dp[i+j]; } } printf("Case %d: %.6lf ",ttt,dp[1]); } }
T11 Easy Game
有一个子序列,有两个人轮流取,每次可以从左到右或从右到左取任意长度的数,使先取的与后取的差最大,并输出这个差。
一开始感觉是道博弈题啊。。。然后立马想到好像传说有博弈dp这种操作,但我太菜了不会啊!
不管怎么样,我们要对出题人有足够的信仰。
先想想策略吧,当前情况下无非是从左去或从右取两种操作,但如果只是取能取的最大值必然有后效性,诸如样例1
假设现在只有一个点,那么因为先手所以必须要拿,
如果有两个呢?考虑要么两个都拿,要么拿左边一个,要么拿右边一个。
如果有三个呢?要么全拿,要么拿左边两个,要么拿一个,而如果拿了一个,后者能取得的最优解就是去掉这一个以后拿两个的方案。显然右边也是如法炮制。
如果四个呢?对于先拿一个、两个的情况,后手的最优策略同样如上。
然后瞬间明了,这原来是道区间dp。。。
用dp[i][j]来表示i-j的区间中的最大差。
显然dp[i][i]就是a[i],然后假设sum[i][j]存的是i-j的前缀和(这只是为了方便理解,事实一维即可)
结合上面的推导
dp[i][j]=max{sum[i][j],sum[i][k]-dp[k+1][j],sum[k+1][j]-dp[i][k]}(i<=k<j)
代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 110 #define INF 0x3f3f3f3f int dp[N][N],a[N],sum[N]; int n,t; int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; memset(dp,0,sizeof(dp)); memset(a,0,sizeof(a)); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); sum[i]=sum[i-1]+a[i]; } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { dp[i][j]=-INF; } dp[i][i]=a[i]; } for(int k=2;k<=n;k++) { for(int i=1;i+k-1<=n;i++) { int j=i+k-1; dp[i][j]=sum[j]-sum[i-1]; for(int mid=i;mid<j;mid++) { dp[i][j]=max(dp[i][j],sum[mid]-sum[i-1]-dp[mid+1][j]); } for(int mid=j;mid>i;mid--) { dp[i][j]=max(dp[i][j],sum[j]-sum[mid-1]-dp[i][mid-1]); } } } printf("Case %d: %d ",ttt,dp[1][n]); } return 0; }
T12 Fast Bit Calculation
一个数字在二进制下,如果一个1的右边还是1,则权值+1
诸如 11011 权值为2,11111权值为4
然后给你一个数x,求1-x之间所有数的权值之和
显然是数位dp,然而yyk大佬告诉我,我实在是太naive了,这道题可以用递推做!
想来也是,其实数位dp究其根源也只是一种暴力。
我们假设sum[i]表示1-i的权值和
那么
Sum[0]=0
Sum[1]=0
Sum[3]=1
Sum[7]=4
这几个数据还是可以手模出来的
然后对于下面该怎么办呢?
比如要算sum[15]
那么15比7要多了一个二进制位,所以说对于该位为0或1都存在sum[7]
所以sum[15]中首先包含两个sum[7]
而如果第四位和第三位都为1则会再多做一个贡献。而这些个数总共有2^(i-2)个,也就是前两位都确定了,后面几位的所有排列数
所以
Sum[15]=2*sum[7]+2^(i-2)
当然这个公式是针对每个2^i-1才有用的。
那普通的该怎么算呢?
显然如果对于一个二进制形式的数首位为1说明此位为0的情况是全被包含的
ans+=sum[i<<len]
然后删去这一位继续处理剩下的位数,就ok了!
代码:
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; long long a[35]; int n,t; void db() { a[0]=0; a[1]=0; a[2]=1; a[3]=4; for(int i=4; i<=31; i++) { a[i]=(1<<(i-2))+(a[i-1]<<1); } } long long get() { int temp=n; long long ans=0,x=1; for(int i=31; i>=1; i--) { if(temp&(x<<i)) { n^=(x<<i); ans+=a[i]+max((long long)0,n-(x<<(i-1))+1); } } return ans; } int main() { int ttt=0; db(); scanf("%d",&t); while(t--) { ttt++; scanf("%d",&n); printf("Case %d: %lld ",ttt,get()); } return 0; }
T13 Generating Palindromes
给你一个字符串,可以在任意位置插任意个字母,求至少插几个字母后会产生回文串?
这道题又是套路。。。
不过由于T8比较敷衍,还是好好讲讲吧。。。(然后讲错了)
对于每1个字母,都是回文串,并不需要任何操作。
2个字母,如果相等自然是0,不等是1
3个字母,如果左右相等,就是1个字母的方案。如果不相等,就是左边取2个的方案加补第三个或者右边取两个加补第一个。
4个字母,如果左右相等,就是第2个字母的方案。如果不相等,就是取左边3个加补第4个或、取右边3个加补第1个
综上所述
状态转移方程就可以推出来了
设dp[i][j]表示i-j之间全部处理成回文串的花费。
则
(s[i]==s[j])
Dp[i][j]=dp[i+1][j-1]
(s[i]!=s[j])
Dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1
代码:
#include<cstdio> #include<string> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 110 int dp[N][N],t,ttt; int main() { scanf("%d",&t); while(t--) { char s[N]; ttt++; memset(dp,0,sizeof(dp)); cin>>s+1; int len=strlen(s+1); for(int i=len;i>=1;i--) { for(int j=i+1;j<=len;j++) { dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1; if(s[i]==s[j]) { dp[i][j]=min(dp[i][j],dp[i+1][j-1]); } } } printf("Case %d: %d ",ttt,dp[1][len]); } }
T14 A Refining Company
在新日暮里中生活着一群快乐的比利和VAN様,但由于他们天天摔跤,产生的DARK值已经快把新日暮里毁掉了!作为新日暮里的管理者,你需要把比利送向西边,VAN様送向北边,
已知新日暮里是一个N*M的矩形,每个1*1的格子里都有一定数量的比利和VAN様,现让你安排一些大巴车,这些大巴车的起点可以在任意位置,但方向只能向西或向北,不能拐弯。
如果向北,沿途的所有比利可以上车。如果向西,沿途的所有比利可以上车。为了防止他们越车摔跤,任意两个公交车的路线不能相交,求能安置好的比利和VAN様的最大数量
这是一道水题( ・´ω`・ ),思路非常简单。
几乎是一眼出方程系列:
Dp[i][j]=max(dp[i-1][j]+sum_line[i][j],dp[i][j-1]+sum_row[i][j])
代码:
#include<cstdio> #include<string> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,m,t; int a,b,suma[505][505],sumb[505][505]; long long dp[505][505]; int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; memset(suma,0,sizeof(suma)); memset(sumb,0,sizeof(sumb)); memset(dp,0,sizeof(dp)); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { scanf("%d",&a); suma[i][j]=suma[i][j-1]+a; } } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { scanf("%d",&b); sumb[i][j]=sumb[i-1][j]+b; } } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { dp[i][j]=max(dp[i][j-1]+sumb[i][j],dp[i-1][j]+suma[i][j]); } } printf("Case %d: %d ",ttt,dp[n][m]); } }
T15 Agent 47
开局只有一个人一把枪,装备全靠打。
告诉你n个小怪的血量以及他们的装备能对其他小怪的伤害,你一开始的武器只能对任何一个小怪造成1点伤害,打死一个小怪后能获得他的装备,并用来打其他的小怪。求消灭所有小怪的最少枪数。
因为n很小,只有15,所以理所应当地想到了状态压缩动态规划
假设一个状态sta中1表示已经被打死的小怪,0表示还没有打死
每次转移显然是从当前状态中挑出一个打死,花费是小怪血量除以当前所有武器中的最大值
然后更新加上这个被打死的小怪的状态
转移方程:设t为打死小i的最小次数
Dp[sta|(1<<i)]=min(dp[sta|(1<<i)],dp[sta]+t)
代码:
#include<cstdio> #include<cstring> #include<algorithm> #define N (1<<15)+10 #define INF 0x3f3f3f3f using namespace std; int dp[N],hp[22],map[22][22],n; char line[20]; int main() { int t,k=0; scanf("%d",&t); while(t--) { k++; memset(dp,INF,sizeof(dp)); scanf("%d",&n); for(int i=0;i<n;i++) { scanf("%d",&hp[i]); dp[1<<i]=hp[i]; } for(int i=0;i<n;i++) { scanf("%s",line); for(int j=0;j<n;j++) { map[i][j]=line[j]-'0'; } } int maxsta=(1<<n)-1; for(int sta=1;sta<=maxsta;sta++) { for(int j=0;j<n;j++) { if(sta&(1<<j)) { continue; } dp[sta|(1<<j)]=min(dp[sta]+hp[j],dp[sta|(1<<j)]); for(int x=0;x<n;x++) { if((sta&(1<<x))&&map[x][j]) { int tot=hp[j]/map[x][j]; if(hp[j]%map[x][j]) { ++tot; } dp[sta|(1<<j)]=min(dp[sta]+tot,dp[sta|(1<<j)]); } } } } printf("Case %d: %d ",k,dp[maxsta]); } }
T16 Palindrome Partitioning
给你一个字符串,要求你划分使所有的子串都是回文串,求最小划分数
好吧并不想多解释了,直接上代码:
#include<cstdio> #include<algorithm> #include<cstring> #define INF 0x3f3f3f3f #define N 1010 using namespace std; char s[N]; int dp[N]; bool judge(int i,int j) { while(i<=j) { if(s[i]!=s[j]) { return 0; } i++; j--; } return 1; } int main() { int t,ttt=0; scanf("%d",&t); while(t--) { ttt++; scanf("%s", s); int len=strlen(s); for(int i=0;i<len;i++) { dp[i]=INF; for (int j=0;j<=i;j++) { if(judge(j,i)) { if(j == 0) { dp[i]=1; } else { dp[i]=min(dp[i],dp[j-1]+1); } } } } printf("Case %d: %d ",ttt,dp[len-1]); } }
T17Neighbor House
这道题比T1还水。。。不说了,
上代码:
#include<queue> #include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int dp[30][3],a[30][3],n,t,ans; int main() { int ttt=0; scanf("%d",&t); while(t--) { ttt++; ans=0; scanf("%d",&n); for(int i=1;i<=n;i++) { dp[i][0]=dp[i][1]=dp[i][2]=0x3f3f3f3f; } for(int i=1;i<=n;i++) { for(int j=0;j<3;j++) { scanf("%d",&a[i][j]); } } for(int i=1;i<=n;i++) { dp[i][0]=min(dp[i-1][1]+a[i][0],dp[i-1][2]+a[i][0]); dp[i][1]=min(dp[i-1][0]+a[i][1],dp[i-1][2]+a[i][1]); dp[i][2]=min(dp[i-1][0]+a[i][2],dp[i-1][1]+a[i][2]); } ans=min(dp[n][0],min(dp[n][1],dp[n][2])); printf("Case %d: %d ",ttt,ans); } }
终于打完了。。。orz