最近做题经常会遇到大佬出题为了避免精度问题要求将答案模一个大质数.然后我就一脸懵逼的连续爆了好几场零.终于下定决心来学一下什么是乘法逆元.其实又感觉不是很难(但为啥比赛就写不出来qwq)
铺垫知识:
费马小定理:
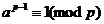
反正就当会证了,开始推导:
首先易知:
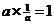
这个不管在正常意义下还是模算术意义下都是正确的
所以:
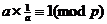 (1)
(1)
然后我们知道:
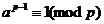
拆分一下:
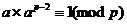 (2)
(2)
联立(1)(2)就得到了
在模p意义下
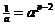
即a的逆元为当然p必须是整数.
但p很大啊...怎么算呢?
当然是kasumi了(雾)
也就是快速幂,不过基于某些原因我程序中会以kasumi呈现
那怎么求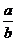 mod p呢?
mod p呢?
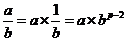
所以就可以打程序了!
代码如下:(求a/b%mod的值)
#include<cstdio> using namespace std; long long a,b,ans,mod; long long kasumi(long long x,long long t) { x=x%mod; long long ans=1; while(t) { if(t&1) { ans=ans*x%mod; } t>>=1; x=x*x%mod; } return ans; } int main() { scanf("%lld%lld%lld",&a,&b,&mod); b=kasumi(b,mod-2); ans=a*b%mod; printf("%lld",ans); }
每天刷题身体棒棒!