国庆结束，学习开始。完成算法作业。

第一题：斐波那契数列（Fibonacci Sequence），又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……。在数学上，斐波纳契数列以递推的方法定义为：F(1)=1，F(2)=1，F(n)=F(n-1)+F(n-2)（n≥2，n∈N）。计算斐波那契数列第n项的值。

要求输出为长整型，不输出小数位数。

#include <stdio.h>

int main()
{
    int n = 0;                    // 输入的整数n(1<=n<=60)
    int i = 0;                    // 循环变量

    scanf("%d", &n);            // 输入

    double a = 1;                // Fibonacci数列的前一项
    double b = 1;                // Fibonacci数列的后一项

    double temp = 0;            // 临时变量

    // 从第三项开始算起，前两项均是1 
    for (i = 3; i <= n; i++)
    {
        temp = a;
        a = b;
        b = temp + a;
    }

    // 输出
    printf("%.0f
", b);

    return 0;
}

第二题 ：全排列问题

请编写程序输出前n个正整数的全排列（n<10），并通过9个测试用例（即n从1到9）观察n逐步增大时程序的运行时间。

输入格式:

给出一个正整数n（<10）。

输出格式:

输出1到n的全排列。每种排列占一行，数字间无空格。排列的输出顺序为字典序，即序列a​1​​,a​2​​,⋯,a​n​​ 排在序列b​1​​,b​2​​,⋯,b​n​​之前，如果存在k使得a​1​​=b​1​​,⋯,a​k​​=b​k​​ 并且 a​k+1​​<b​k+1​​。

/************************************************************************/
/* 全排列组合                                                           */
/************************************************************************/
#include <stdio.h>

/************************************************************************/
/* 函数申明                                                             */
/************************************************************************/
int has_num(int num, int flag[], int n);
void set_flag(int flag[], int n, int is_used);

/************************************************************************/
/* 主函数                                                               */
/************************************************************************/
int main()
{
    // 标记位：1-9存储数据1-9，下标0空位
    int flag[10] = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
    int i = 0;                // 循环变量
    int n = 0;                // 输入的数
    int start = 0;            // 开始的数
    int end = 0;            // 结束的数

    // 输入
    scanf("%d", &n);

    // 计算开始的数，例如：如果n是4，则算到1 2 3 0
    for (i = 1; i <= n - 1; i++)
    {
        start = (start + i) * 10;
    }
    // 加最后一位n， 1234
    start += n;

    // 计算结束的数，如果n是4，则为4 3 2 0
    for (i = n; i >= 2; i--)
    {
        end = (end + i) * 10;
    }
    // 加最后一位n，4321
    end += 1;

    // 输出全排列
    while (start <= end)
    {
        // 如果是全排列的数，则输出
        if (has_num(start, flag, n) == 0)
        {
            printf("%d
", start);
        }

        // start++
        start++;

        // 置回数组为未标记状态
        set_flag(flag, n, 0);
    }
    

    return 0;
}

/************************************************************************/
/* 判断是否有该数字是否为全排列数字                                     */
/* 即：判断该数子的各个位是否重复                                        */
/* -1错误 0正确                                                            */
/************************************************************************/
int has_num(int num, int flag[], int n)
{
    int a = num;
    int temp = 0;

    while (a != 0)
    {
        temp = a%10;
        
        // 判断是不是超过了n或者为0
        if ((temp > n) || (temp == 0))
        {
            return -1;
        }

        // 该位置数字还未出现
        if (flag[temp] != 1)
        {
            flag[temp] = 1;
        }
        else
        {
            // 该位数字已经使用
            return -1;
        }

        a /=10;
    }

    // 正确
    return 0;
}

/************************************************************************/
/* 设置标记位                                                           */
/* is_used    0:未用 1:使用                                                */
/************************************************************************/
void set_flag(int flag[], int n, int is_used)
{
    int i = 0;

    for (i = 0; i <= n; i++)
    {
        flag[i] = is_used;
    }
}

第三题 ：ACKERMAN函数

有两个整型变量m、n，Ackerman函数A(n，m)定义如下：

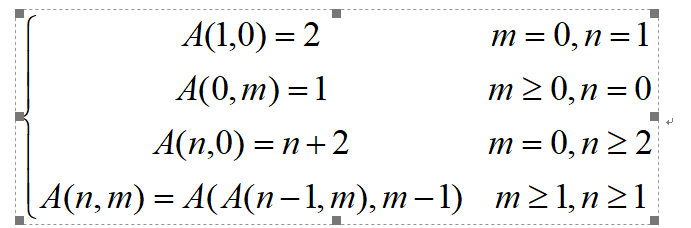 从键盘输入适当整数n,m值，计算Ackerman函数A(n,m)的值。

输入格式:

在一行中输入2个正整数A和B，并用空格分隔。

输出格式:

输出Ackerman函数值。

#include <stdio.h>

// 全局变量
int ACK[1000][1000] = {0};

// 函数声明
int Ackerman(int n, int m);


int main()
{

    int n = 0;
    int m = 0;

    // 输入
    scanf("%d%d", &n, &m);

    // 计算并输出
    printf("%d
", Ackerman(n, m));

    return 0;
}


int Ackerman(int n, int m)
{
    // 先判断是否计算过
    if (ACK[n][m] != 0)
    {
        return ACK[n][m];
    }

    // n = 1, m = 0
    if ((n == 1) && (m == 0))
    {
        return ACK[n][m] = 2;
    }

    // n = 0, m >= 0
    if ((n == 0) && (m >= 0))
    {
        return ACK[n][m] = 1;
    }

    // n >= 2, m = 0
    if ((n >= 2) && (m == 0))
    {
        return ACK[n][m] = n + 2;
    }

    return ACK[n][m] = Ackerman(Ackerman(n - 1, m), m - 1);

}

第四题：汉诺塔问题

古代某寺庙中有一个梵塔，塔内有3个座A、B和C，座A上放着64个大小不等的盘，其中大盘在下，小盘在上。有一个和尚想把这64 个盘从座A搬到座B，但一次只能搬一个盘，搬动的盘只允许放在其他两个座上，且大盘不能压在小盘上。现要求用程序模拟该过程，输入一个正整数n，代表盘子的个数，编写函数

void hanoi(int n,char a,char b,char c)

其中，n为盘子个数，从a座到b座，c座作为中间过渡，该函数的功能是输出搬盘子的路径。

输入格式:

输入在一行中给出1个正整数n。

输出格式:

输出搬动盘子路径。

/************************************************************************/
/* 7-6 汉诺（Hanoi）塔问题                                              */
/************************************************************************/
#include <stdio.h>

/************************************************************************/
/* 函数声明                                                             */
/************************************************************************/
void hanio(int n, char a, char b, char c);

/************************************************************************/
/* 主函数                                                               */
/************************************************************************/
int main()
{
    int n = 0;

    // 输入盘子数
    scanf("%d", &n);

    // 函数调用
    hanio(n, 'a', 'b', 'c');

    return 0;
}

/************************************************************************/
/* 汉诺塔函数                                                           */
/************************************************************************/
void hanio(int n,char a,char b,char c)
{
    if(n == 1)
    {
        printf("%c-->%c
", a, b);        //递归出口
    }
    else
    {
        hanio(n-1, a, c, b);            //把n-1个盘子从A搬到C
        printf("%c-->%c
", a, b);
        hanio(n-1,c, b, a);                //把n-1个盘子从C搬到B
    }
}

第五题 ：众数与重数问题

给定含有n个元素的多重集合S，每个元素在S中出现的次数称为该元素的重数。一般来说，多重集S中重数最大的元素为众数。例如，S={1,2,2,2,3,5}，S的众数是2，其重数为3。但是，如果有两个或两个以上的数出现次数都是最多的，那么这几个数都是这组数据的众数。例如：1，2，2，3，3，4的众数是2和3，并按众数在集合中出现的先后次序输出。如果所有数据出现的次数都一样，那么这组数据没有众数。例如：1，2，3，4，5没有众数。 对于给定的由n（n<2000)个自然数组成的多重集S，计算S的众数及其重数。

输入格式:

输入在一行中给出多重集S中的元素个数n；在接下来的n行中，每行有一个自然数。

输出格式:

有众数输出有2行，第1行是众数，第2行是重数。 无众数输出字符串"no mode."

输入样例1:

输入样例如下：

6
1
2
2
2
3
5

输出样例1:

输出样例如下：

2
3

输入样例2:

输入样例如下：

6
1
2
2
3
3
5

输出样例2:

输出样例如下：

2 3
2

输入样例3:

输入样例如下：

6
1
2
4
3
5
6

输出样例3:

输出样例如下：

no mode.

import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedHashMap;
import java.util.List;
import java.util.Map.Entry;
import java.util.Scanner;

/**
 * 众数问题
 * @author root
 * 1. hash表 时间复杂度为O(n)，但空间占用较大，此算法使用该解法
 * 2. 排序 对元素表进行排序，然后统计元素出现的个数，得出众数。时间复杂度为O(nlgn)，空间复杂度为O(n) 
 * 3. 二叉搜索树 用rbtree之类的树来实现。如果实现的好，复杂度和排序接近。
 * 4. 改写快速排序
 */
public class Main {
    /**
     * 主函数
     * @param args
     */
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt();                // 输入待输入数字集合的个数
        
        // 输入数字集合并遍历寻找众数
        int multiple = 0;                                    // 重数
        HashMap<Integer, Integer> inputSet = new LinkedHashMap<Integer, Integer>();
        
        for (int i = 0; i < n; i++) {
            int key = scanner.nextInt();
            int value = 1;
             
            if (inputSet.containsKey(key)) {
                value = inputSet.get(key) + 1;
            }
            
            // 找到出现次数最多的数
            if (value > multiple) {
                multiple = value;
            }
            
            // 将该数与该数的众数加入hash表
            inputSet.put(key, value);
        }
        
        // 输出众数并统计重数
        List<Integer> modes = new ArrayList<Integer>();        // 众数集合
         
        // 将出现次数最多的数放入List集合
        for (Entry<Integer, Integer> entry : inputSet.entrySet()) {
            if (entry.getValue() == multiple) {
                modes.add(entry.getKey());
            }
        }
        
        // 所有的数均是众数，那即是没有众数，输出no mode.
        if (modes.size() == inputSet.size()) {
            System.out.println("no mode.");
            
            return;
        }
        
        boolean flag = true;                                // 标记是不是第一个输出的，方便输出空格
        for (Integer integer : modes) {
            if (flag) {
                System.out.print(integer);
                flag = false;
            } else {
                System.out.print(" " + integer);
            }
        }
        System.out.println();
        System.out.println(multiple);
        
    }
}