代码:
#include <iostream>
using namespace std;
const int M = 100; //设物品最多100个
int n, MaxWight, SumValue;
int wight[M], value[M], ans[M], a[M];
void backtrack(int t, int Swight, int Svalue)
{
// cout << t << " " << Swight << " " << Svalue << endl; 调试的时候可以输出数据做参考
if (t >= n)
{
if (SumValue < Svalue)
{
SumValue = Svalue;
for (int i = 0; i < n; i++)
ans[i] = a[i];
}
}
else
{
for (int i = 0; i <= 1; i++)
{
a[t] = i;
Swight = Swight + i * wight[t];
Svalue = Svalue + i * value[t];
if (Swight <= MaxWight)
{
backtrack(t + 1, Swight, Svalue);
}
else //实际重量大于最大重量时,从背包把物品拿出。
{
Swight = Swight - i * wight[t];
Svalue = Svalue - i * value[t];
}
}
}
}
int main()
{
cin >> n >> MaxWight;
for (int i = 0; i < n; i++)
cin >> value[i];
for (int i = 0; i < n; i++)
cin >> wight[i];
backtrack(0, 0, 0);
for (int i = 0; i < n; i++)
cout << ans[i];
cout << endl
<< SumValue << endl;
return 0;
}
n 代表的是物品个数
MaxWight 背包能装的最大体积
SumValue 物品的最大价值
ans 数组,最终选择方式
a 数组,临时选择方式
思路:物品只有两种选择,放或者不放,构造二叉树,n 个物品就是 n 层树,然后进行最优值更新。
样例:
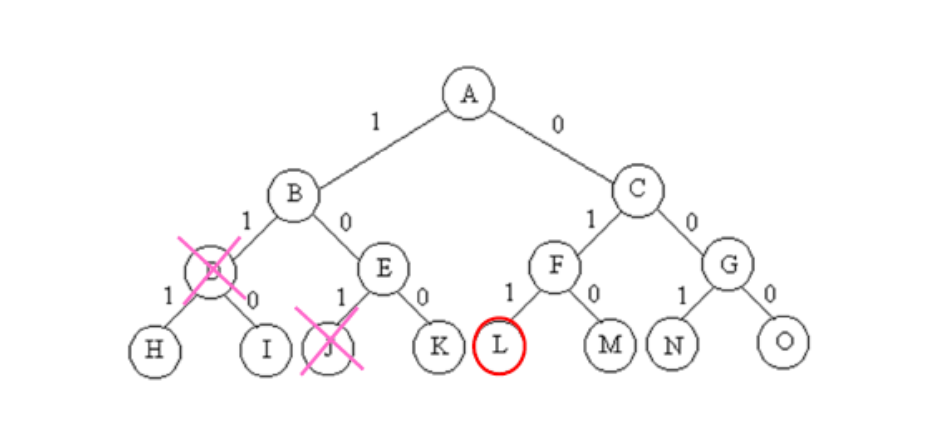
图1
背包构造出的二叉树如图1,顺序三从右边到左边,也就是先不放物品,然后再慢慢放进去。
输入:
3 30
45 25 25
16 15 15
输出: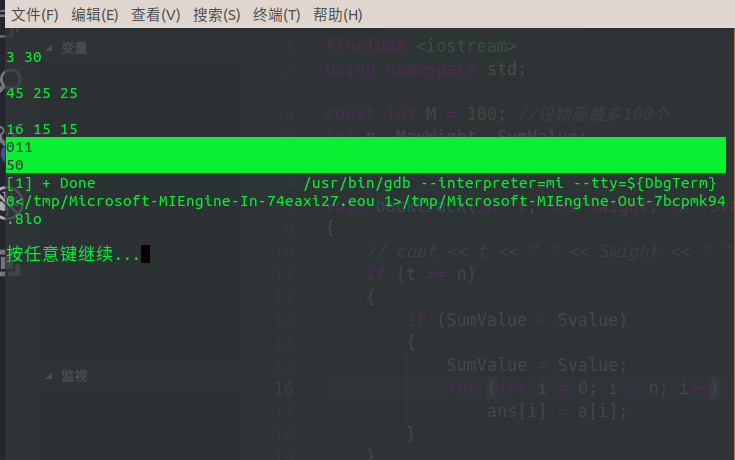
0 1 1 :放进后面 2 件物品。 50 : 最大价值
附回溯法搜索子集树模板:
void backtrack(int k)
{
if(到达边界) 更新或者输出结果
else
{
对于每一种可能进行操作(for循环 i)
{
if(限定条件合法)
backtrack(k+i);
}
}
}