有n种物品,每种物品的体积是ci,价值是wi,数量不限,现在有一个容积是v的背包,如何装物品才能使价值最大。
这个题与0-1背包很像,或者说是0-1背包的升级版。原来物品有两个状态可选,0和1;现在有v/ci+1个状态可选,0(不装),1(装一个),2(装两个)……v/ci(装v/ci个)。
那么把0-1背包的推导方程扩展一下就变成了
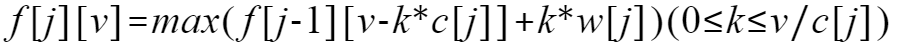
k的取值是0和1的时候,就是0-1背包问题。我们能不能用0-1背包的思路呢?答案是肯定的。下面是递归调用的方法
void zobag(vector<int>& weights, vector<int>& wealths, int vbag, int index, map<int, int>& selmap) { if (index < 0) { return; } else { map<int, int> selmap2 = selmap; for (int i = 0; i <= vbag / weights[index]; i++) { map<int, int> selmap1 = selmap; if (vbag >= i * weights[index]) { selmap1[index] = i; } zobag(weights, wealths, vbag - i * weights[index], index - 1, selmap1); int tmp1 = 0; int tmp2 = 0; //int tmpw1 = 0; for (auto& iter : selmap1) { int a = iter.second; while (a > 0) { tmp1 += wealths[iter.first]; //tmpw1 += weights[iter.first]; a--; } } for (auto& iter : selmap2) { int a = iter.second; while (a > 0) { tmp2 += wealths[iter.first]; a--; } } /*if (tmpw1 != 10) { tmp1 = 0; selmap1.clear(); }*/ if (tmp1 > tmp2) { selmap2 = selmap1; } } selmap = selmap2; } } int main() { int vbag = 10; vector<int> weights = { 5, 3, 4, 3, 5 }; vector<int> wealths = { 500, 200, 300, 350, 400 }; map<int, int> selmap; zobag(weights, wealths, vbag, weights.size() - 1, selmap); for (auto& iter : selmap) { int a = iter.second; while (a > 0) { cout << iter.first << endl; a--; } } char inchar; cin >> inchar; }
输出是3 3 3,也就是索引是3(第四种物品)放3个。我们看到第四种物品是350/3,所以放三个是9的空间,小于给定的10,并且是最大的。
我们把循环的条件从vbag/weights[index]改成1,就是0-1背包。
注释的部分是另一种问题,就是求如果必须要求正好装满背包,不能多,也不能少,那么输出就是0 0。只要我们这个写好了,其他的都是增加额外的判断条件就好了。
如果单单是完全背包问题,可以进行优化,就是把同体积价值小的去掉;或者在转成0-1背包问题的时候,把物品改成w*2^k形式。比如物品是500/3(价值500,体积3),原来拆分是改成多个500/3,现在可以改成500/3 1000/6……这样的话可以减少递归的次数,因为原来计算两次500/3,现在只需计算一次1000/6就可以。
这样总感觉不是特别好,那么我们原来动态规划的方法可以用吗?答案也是肯定的
int main() { int vbag = 10; vector<int> weights = { 5, 3, 4, 3, 5 }; vector<int> wealths = { 500, 200, 300, 350, 400 }; int* dp = new int[(10 + 1) * 5]();//多一个,方便用索引直接表示内容 int maxdp = 0; int maxi = 0; int maxj = 0; for (int vbgi = 0; vbgi < 10 + 1; vbgi++) { for (int i = 0; i < 5; i++) { if (vbgi == 0) { *(dp + vbgi * 5 + i) = 0; } else { int optw = 0; int wi = 0; while (vbgi >= weights[i] * wi) { int tmpoptw = wealths[i] * wi; if (i - 1 >= 0) { tmpoptw = tmpoptw + *(dp + (vbgi - weights[i] * wi) * 5 + i - 1); } if (tmpoptw > optw) { optw = tmpoptw; } wi++; } if (optw > maxdp) { maxdp = optw; maxi = i; maxj = vbgi; } //这里注意赋值 *(dp + vbgi * 5 + i) = optw; } } } while (*(dp + maxj * 5 + maxi) > 0 && maxi >= 0 && maxj >= 0) { //这里需要遍历找到第一个满足的条件,因为后面的会取前面的最大值 for (int i = 0; i < maxi; i++) { if (*(dp + maxj * 5 + i) == *(dp + maxj * 5 + maxi)) { maxi = i; break; } } //这里注意从1开始遍历,因为表示装了几个 for (int i = 1; i <= *(dp + maxj * 5 + maxi) / wealths[maxi]; i++) { cout << wealths[maxi] << endl; } maxj = maxj - *(dp + maxj * 5 + maxi) / wealths[maxi] * weights[maxi]; maxi--; } char inchar; std::cin >> inchar; }
动态规划就是在原来的基础上加上一个循环,把一个物品多次加入就可以了。