排列组合

参考

https://www.cnblogs.com/graphics/archive/2011/07/14/2105195.html

https://zhuanlan.zhihu.com/p/79863106

https://zh.wikipedia.org/wiki/%E7%BB%84%E5%90%88%E6%95%B0%E5%AD%A6

我们在做算法题的时候，很多时候需要用到穷举，排列组合，获得所需的结果。然后再根据这个增加条件，慢慢减少判断次数，就是动态规划。所以我们先弄清楚如何排列组合。

给定字符串s，求出s所有可能的子串。

int main()
{
    string a = "abcdef";
    string b = "acdfg";
    string c = "abc";
    int n = 1 << c.size();
    for (int i = 0; i < n; i++)
    {
        int j = i;
        string tmp;
        for (auto iter = c.rbegin(); iter != c.rend(); iter++)
        {
            if (j & 1)
            {
                tmp = *iter + tmp;
            }
            j = j >> 1;
        }
        cout << tmp << endl;
    }
    char inchar;
    cin >> inchar;
}

这个解法，就是根据每一个元素，都有两种状态，在子串中，或是不在子串中。那么一个n个字符串，就会有2^n个组合。用一个二进制进行判断，每次右移1，个位置上是1的表示这次存在于子串。只不过这是倒叙的，需要反过来。

这里的局限性就是，只能保存int的32位的字符串，如果是64位，也只能保存64个字符的字符串。再长的字符串就不行了，但是我们考虑到64个字符的字符串的所有组合情况，已经是天文数字了，在实际情况中，我们也不会碰到。碰到之后肯定有其他的解法。

问题扩展，从n个元素中，选长度是m（m<=n）子串的组合。按照大家总结的规则，c(n,m)表示从n个字符串中取m个长度所有的子串情况，那么c(n,m)=c(n-1,m) + c(n-1, m-1)。解释就是当我要判断第n个元素加进来的子串情况时，只需要知道前n-1个子串的所有情况，再加上当前子串的情况，就可以得出最后的答案。前面n-1子串的情况，可以分为，第n个计算在内，那么就是c(n-1, m-1)和第n个不计算在内就是c(n-1,m)。

比如abc，那么选择c(3,2)=c(3-1,2) + c(3-1, 2-1)。那么就是ab和a b，然后ab是不需要加c，a和b需要加c，就是ab ac bc。也就是计算第n个情况的时候，肯定需要先计算出n-1的情况，n-1的情况中包含了m个数，n就不用计算在内；包含了m-1的情况，就把m-1所有的情况都加上第n个元素。

struct MNODE
{
    string substr;
    MNODE* pnext;
    MNODE()
    {
        pnext = nullptr;
    }
};
MNODE* msubstr(string& srcstr, int index, int sublen)
{
    MNODE* tmpp = nullptr;
    MNODE* prep = nullptr;
    if (index >= sublen && sublen > 0)
    {
        if (sublen == 1)
        {
            for (int i = 0; i < index; i++)
            {
                MNODE* ftpn = nullptr;
                if (tmpp == nullptr)
                {
                    tmpp = new MNODE;
                    prep = tmpp;
                    ftpn = tmpp;
                }
                else
                {
                    ftpn = new MNODE;
                    prep->pnext = ftpn;
                    prep = ftpn;
                }
                ftpn->substr = srcstr[i];
            }
        }
        else if (sublen > 1)
        {
            MNODE* nsub = msubstr(srcstr, index - 1, sublen - 1);
            tmpp = nsub;
            while (nsub != nullptr)
            {
                nsub->substr = nsub->substr + srcstr[index - 1];
                prep = nsub;
                nsub = nsub->pnext;
            }
            nsub = msubstr(srcstr, index - 1, sublen);
            prep->pnext = nsub;
            while (nsub != nullptr)
            {
                nsub = nsub->pnext;
            }
        }
    }
    return tmpp;
}
int main()
{
    string a = "abcdef";
    string b = "acdfg";
    string c = "abcd";
    MNODE* psubstr = msubstr(a, a.size(), 3);
    while (psubstr != nullptr)
    {
        cout << psubstr->substr << endl;
        MNODE* tmpp = psubstr;
        psubstr = tmpp->pnext;
        delete tmpp;
    }
    char inchar;
    cin >> inchar;
}

按照公式推导，遇到索取的子字符串是1的时候，达到边界，可以求值退出，后面在前面的基础上增加当前的字符，不断累加，到最后得出结果。

排列就是从n中选k，相同的元素，顺序不同，也算不同的一种，数学中排列的公式是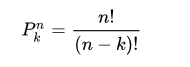

如果选取的k个元素是可以重复的，那么就是，因为每次选择都是n个元素，可以选k次，所以就是n*n*n...*n，k个n种选择相乘。

组合就是选择的元素，位置不同没有影响，比如从一堆球中选择不同颜色球的组合，数学中的组合公式是

与排列类似，因为肯定还是需要取那么多种类，只不过要把重复的去掉，就再除以k的阶。

如果是选取的元素可以重复，组合的公式就是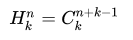需要额外加上重复的选择。这个公式可以转换成另一个

那我们上面的2^n是如何得到的呢？来源于这个公式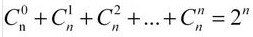，我们可以知道，获取子串，虽然与顺序有关，但是，我们不能倒序获取或是从中间任意一个位置获取，字符串是有顺序的，获取的其他顺序的字符串不能算是子串。也就相当于获取固定索引位置的字符串，只能按照原来的顺序组成一个子串，不可能出现多个，也就是组合，按照这个公式，就是2^n。