动态规划1-国王和金矿

参考

https://juejin.im/post/5a29d52cf265da43333e4da7

有一个国家发现了5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖，要么不挖 ，不能派出一半人挖取一半金矿。要求如何分配工人才能挖出最多的黄金。

第一座金矿含金500，需要5人；第二座金矿含金200，需要3人；第三座金矿含金300，需要4人；第四座金矿含金350，需要3人；第五座金矿含金400，需要5人。

最开始想到的是，算每个金矿的含金量与需要工人的比例，也就是每个人可挖金的数量，按照从大到小，排序，选取最大的。但是我们现在人数固定，并不是人数不限。所以有可能第一个满足了，导致后面的人没法挖矿或是挖了一个更少的，抵消了前面的优势。所以这里还是要算出每种情况，求最优解。

这个问题的话，按照分解，求第五个金矿最大值，就是求挖当前金矿和剩下的人挖前面四个金矿与不挖当前金矿和所有人挖前面四个金矿的最大值。f(5) = max(f(4,n), f(4,n-p)+G(5))。可能有人说，既然前四个可以加上第五个，那么肯定加上啊。但是前四个金矿最大值，并不一定是四个全部都挖，为了组合到第五个金矿，有可能为了更少的使用工人，前四个有的金矿没有挖。那么求四座金矿的，就需要求三座金矿的，一直到求一座金矿。

第一种方法就是穷举，把所有情况列出来，然后一个个判断，这样效率最差。

第二种方法就是上面的，根据公式，一层层的找，比如计算n=5，就计算n=4，直到n=1，然后返回。但是这样计算也很麻烦，因为每次计算n，都有一种情况就是把第n座金矿算进去，就是派人去挖第n座金矿，那么总的人数就发生了变化，就意味着前面的要重新遍历计算。

int gold[] = { 500,200,300,350,400 };
int workers[] = { 5,3,4,3,5 };
void dgold(bool* diggold, int index, int pnum)
{
    if (index == 0)
    {
        if (pnum >= workers[0])
        {
            diggold[0] = true;
        }
    }
    else
    {
        bool tmp[5] = { false };
        memcpy(tmp, diggold, 5 * sizeof(bool));
        tmp[index] = false;
        dgold(tmp, index - 1, pnum);
        bool tmp1[5] = { false };
        memcpy(tmp1, diggold, 5 * sizeof(bool));
        if (pnum >= workers[index])
        {
            tmp1[index] = true;
        }
        dgold(tmp1, index - 1, pnum - workers[index]);
        int tmpgold = 0;
        for (int i = 0; i <= index; i++)
        {
            if (tmp[i])
            {
                tmpgold += gold[i];
            }
        }
        int tmpgold1 = 0;
        for (int i = 0; i <= index; i++)
        {
            if (tmp1[i])
            {
                tmpgold1 += gold[i];
            }
        }
        if (tmpgold > tmpgold1)
        {
            memcpy(diggold, tmp, 5 * sizeof(bool));
        }
        else
        {
            memcpy(diggold, tmp1, 5 * sizeof(bool));
        }
    }
}
int main()
{
    bool diggold[5] = { false };
    dgold(diggold, 4, 10);
    char inchar;
    cin >> inchar;
}

这就是递归遍历的方法。我们要取第n座金矿的情况，那么有两种，一个是第n座金矿开采，另外一个是第n座金矿不开采。那么依次递归，计算两个最大值。递归出口就是第一座金矿。

那这道题有其他的解决方法吗？有，那就是动态规划2-最长公共子序列 中讲的，我们先看表

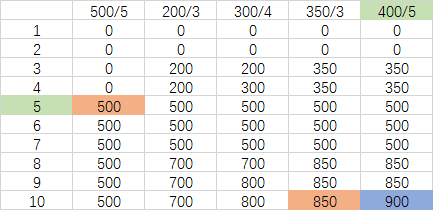
比如标蓝的位置的值，有两个解，一个是前一个850；另一个是400/5对应的400加上，蓝色对应的人数10，减去当前的400/5对应的5人，那就是第5行，从500/5-350/3之间的最大值（就是500），也就是一共是900，那么取最大值，就是900.

感觉与最长公共子序列一样，由上面的推导公式，f(5) = max(f(4,n), f(4,n-p)+G(5))，可知，求第n座金矿的最优解，就等于把当前金矿算进去，然后去掉这座金矿所需的人数，然后查找前n-1的金矿，人数是10-p（p是当前金矿需要的人）对应的数据与自己前一个数据（第n座金矿不计算在内）最大值。这样前面的数据也可以用得到了。代码如下

int gold[] = { 500,200,300,350,400 };
int workers[] = { 5,3,4,3,5 };
int main()
{
    //i is gold j is people
    auto optgold = new int[10 * 5]();
    int maxgold = 0;
    int maxi = 0;
    int maxj = 0;
    for (int j = 0; j < 10; j++)
    {
        for (int i = 0; i < 5; i++)
        {
            if (j + 1 < workers[i])
            {
                if (i - 1 < 0)
                {
                    *(optgold + j * 5 + i) = 0;
                }
                else
                {
                    *(optgold + j * 5 + i) = *(optgold + j * 5 + i - 1);
                }
            }
            else
            {
                int pre = 0;//当前金矿不开采，最大值
                if (i - 1 >= 0)
                {
                    pre = *(optgold + j * 5 + i - 1);
                }
                int mnow = gold[i];//当前金矿开采，最大值
                if (i - 1 >= 0 && j - workers[i] >= 0)
                {
                    mnow = mnow + *(optgold + (j - workers[i]) * 5 + i - 1);
                }
                if (pre > mnow)
                {
                    *(optgold + j * 5 + i) = pre;
                }
                else
                {
                    *(optgold + j * 5 + i) = mnow;
                }
            }
            if (*(optgold + j * 5 + i) > maxgold)
            {
                maxgold = *(optgold + j * 5 + i);
                maxi = i;
                maxj = j;
            }
        }
    }
    maxj++;
    while (maxj > 0)
    {
        for (int i = 0; i <= maxi; i++)
        {
            if (*(optgold + (maxj - 1) * 5 + i) == maxgold)
            {
                maxi = i;
                break;
            }
        }
        cout << "gold " << gold[maxi] << " worker " << workers[maxi] << " gold " << maxi + 1 << endl;
        maxj = maxj - workers[maxi];
        maxgold = maxgold - gold[maxi];
        maxi--;
        
    }
    char inchar;
    cin >> inchar;
}

遇到的问题，一，在计算挖当前矿的时候，忘记把当前矿的金额加进去；二，由于j的索引与人数差一，导致最后遍历输出的时候不方便。