参考
https://www.jianshu.com/p/3d92fe1c34af
https://blog.csdn.net/leonliu06/article/details/78685197
因为做leetcode的一道题整数反转https://leetcode-cn.com/problems/reverse-integer/,中间用到了int的最大值和最小值。很多解题都是直接默认知道int的最大值最小值,或是使用了c++的INT_MAX和INT_MIN宏。如果没有宏,或是题目改成31位数字,30位数字,那岂不是解不了了。本着一切都是通用,都是可以自己计算获得的思想,那怎么求int的最大最小值呢?
(1 << 31) - 1;//最大值2147483647,这里一定要加括号,因为<<的优先级比-低 1 << 31;//最小值-2147483648
另一个问题来了,为什呢?为什么-2147483648 - 1不是-2147483649呢?先看看内存

嗯,就是1向左移动了31位,就是到最高的位置,那么,就是负数最小值,减一,变成了正的最大值,并且如果把负的最小值按照无符号正数输出,实际上是2147483648,减一,正好是2147483647???带着一系列的疑问,我们开始补码之旅。
为什么直接是补码,我感觉一开始讲解原码,然后是反码,最后补码有点本末倒置。因为计算机中只有补码,补码才是最合理的,最应该被了解的,其次才是原码,最后是反码。只不过求补码的一种方式需要借助到反码,具体解释如下
- 原码-十进制数字的二进制形式,只不过最高位用来表示正负
- 反码-符号位不变,负数的原码各位取反,正数保持不变
- 补码-正数不变,负数的补码是其反码加1
我们以四位数字来举例,原码如下
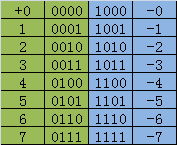
我们看起来很直观,很容易理解,对于计算机可不这么认为。首先,如果保存的是原码,那么就要增加一个寄存器保存这个符号位,增加了开销。其次,加法如果有进位,我们可以一位一位的计算,减法如果有借位呢?有可能会借位好几次,并且是不固定的,那么又需要额外的空间保存。还有就是,出现了两个0,+0和-0,那么在判断0的时候,还需要判断两次。最最重要的是1+(-1)=0001+1001=1010=-2???这……已经不是麻烦的问题了。
为了解决这些问题,补码出现了,因为计算机保存数据的空间有限,比如四位空间,按照原码,只能保存-7~7.那么这里就有一个东西可以利用,就是溢出。四位空间的数据是循环的,不可能有超出这个范围的数据,减掉一个数据获得的值,是不是与加上一个数据转一圈获得的值一样呢?查资料中,有作者给了一个恰当的比喻,就是钟表。比如,当前是6点,那么减去3个小时,是3点,如果是加上9个小时呢,还是3点,虽然多转了一圈,但是因为溢出,像钟表一样,没有区别,补码就是这个意思。这个例子中6-3就等于6+9,那么9就是-3的补码。这样就可以把负数换成正数。减少了一个减法运算器,也减少了减法的运算复杂度。
举例3-2,那么相当于3+(-2),4位空间的数据无符号的话是0-15,也就是以16为进制转一圈,那么回退2个,就相当于加上14个,因为加上16个是正好转了一圈,相当于加了0,那么少加2个呢,就是14个,所以-2的补码就是14,14的二进制是1110(无符号),那么3+14就等于17,17针对于16的模,就是1,正好与3-2一样。这才是补码的真实意义,只不过按位取反再加一,是补码的一种求解方式。中间出现的一个转换过程,把负数的符号位不变,其他位按位取反得到的数据叫做反码。反码的出现也是为了解决这个问题,只不过没有完美的解决,补码弥补上了最后的限制。
反码补码都是为了解决负数提出的,所以呢,正数的反码补码都是原码,没有任何变化。
下面的作者解释了为什么补码的一种求解方法是反码加一
# 按以上理论,减一个数等于加上它的补数,所以 5 - 3 # 等价于 5 + (16 - 3) // 算术运算单元将减法转化为加法 # 用二进制表示则为: 0101 + (10000 - 0011) # 等价于 0101 + ((1 + 1111) - 0011) # 等价于 0101 + (1 + (1111 - 0011)) # 等价于 0101 + (1 + 1100) // 括号内是3(0011)的反码+1,正是补码的定义 # 等价于 0101 + 1101 # 所以从这里可以得到 -3 = 1101 # 即 `-3` 在计算机中的二进制表示为 `1101`,正是“ -3 的正值 3(`0011`)的补码(`1101`)”。 # 最后一步 0101 + 1101 等于 10010 ———————————————— 版权声明:本文为CSDN博主「leonliu06」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/leonliu06/article/details/78685197
这样的话,没有了负数,也就没有了减法,同样,没有乘法,没有除法。只有加法,或是只有位运算。减法就是加上负数,乘法就是循环多次相加,除法,就是循环多次相减,也就是循环相加多次除数的相反数。简化了设计,优化了效率。
下面介绍为什么1<<31是负的最小值,还是拿4位数字表示,上面列出了原码,下面是反码,正数的不变,负数的除了符号位,其他位按位取反。
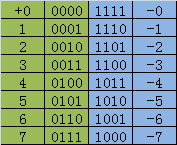
那么补码呢,正数不变,负数在上面获得的反码基础上加一
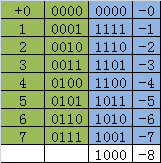
我们可以看到反码不仅解决了负号问题,还解决了+0和-0的问题,+0和-0的反码都是0000,那么我们看到,多了一个1000,那么这个数,就用来表示-8。那么上面的问题就可以解释了1<<31是负数最小值,减一呢,按照位运算,计算机内并没有负数,那就是正的最大值。按照这个4位的数字做例子就是1000,也就是1<<3是-8,最小的负数,减一,变成0111,也就是7,最大的正数。