前言
1977年,德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了这种算法,各种文本编辑器的"查找"功能(Ctrl+F),大多采用此算法。
原理
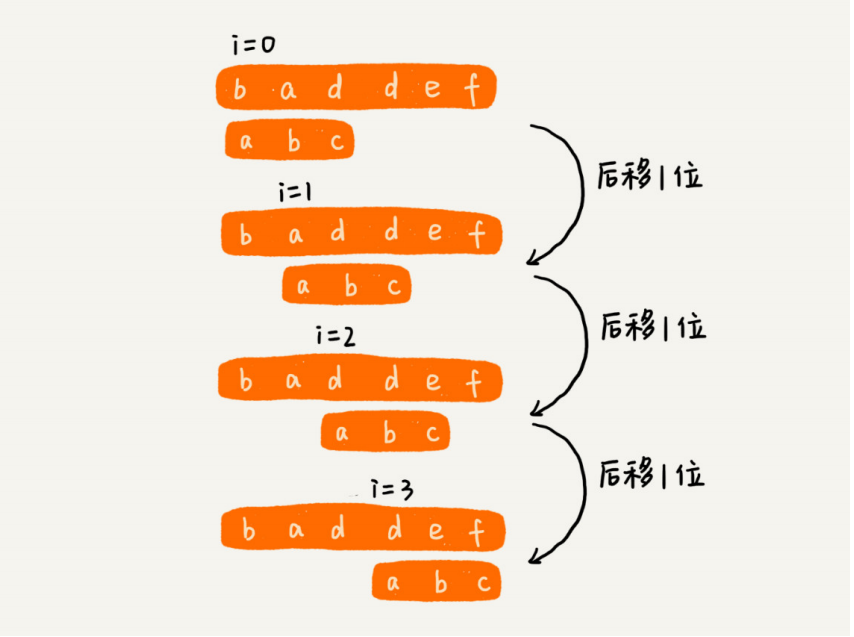
我们使用暴力解法时,是一位一位的向后移动。

当我们遇到上图这种情况,子串最后一个字符E和S不匹配,且S不在待查找子串中,我们就可以直接后移7位,移动到S的下一位。Boyer-Moore算法本质上就是找到如何更快的向后移动的规律。
BM 算法主要包括两部分,坏字符规则和好后缀规则。

字符P和E不匹配,P为坏字符,但P包含在EXAMPLE中,所以后移2位

总结得到坏字符规则:
后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置
如果坏字符不包含在搜索词中,上一次出现位置为-1.
/**
* Boyer-Moore算法,仅支持ASCII码,算法中仅使用了坏字符规则,没有使用好后缀规则
*/
public class BoyerMooreStringMatcher implements StringMatcher {
@Override
public int indexOf(String source, String target) {
int targetLen = target.length();
int sourceLen = source.length();
if (targetLen == 0) {
return 0;
}
if (sourceLen < targetLen) {
return -1;
}
return indexOf(source.toCharArray(), target.toCharArray());
}
private int indexOf(char[] text, char[] pattern) {
if (pattern.length == 0) {
return 0;
}
int[] charTable = makeCharTable(pattern);
for (int i = 0, j; i < text.length - pattern.length + 1; ) {
for (j = pattern.length - 1; pattern[j] == text[i + j]; j--) {
if (j == 0) {
return i;
}
}
//坏字符规则得到的后移位数可能为负数,所以要和1比较
i += Math.max(1, j - charTable[text[i + j]]); //仅使用坏字符规则
}
return -1;
}
/**
* 创建搜索词的哈希表,键为字符的ASCII码值,值为下标
**/
private int[] makeCharTable(char[] pattern) {
final int ALPHABET_SIZE = 256;
int[] table = new int[ALPHABET_SIZE];
for (int i = 0; i < table.length; ++i) {
table[i] = -1;
}
for (int i = 0; i < pattern.length - 1; ++i) {
table[pattern[i]] = i;
}
return table;
}
}
关于好后缀规则,请看 字符串匹配的Boyer-Moore算法 这篇博客。
参考
字符串匹配的Boyer-Moore算法
Boyer Moore Algorithm for Pattern Searching
Boyer Moore Algorithm | Good Suffix heuristic
github开源实现