[Swift-2019力扣杯春季初赛]4. 从始点到终点的所有路径

★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
➤微信公众号：山青咏芝（shanqingyongzhi）
➤博客园地址：山青咏芝（https://www.cnblogs.com/strengthen/）
➤GitHub地址：https://github.com/strengthen/LeetCode
➤原文地址： 
➤如果链接不是山青咏芝的博客园地址，则可能是爬取作者的文章。
➤原文已修改更新！强烈建议点击原文地址阅读！支持作者！支持原创！
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★

给定有向图的边 edges，以及该图的始点 source 和目标终点 destination，确定从始点 source 出发的所有路径是否最终结束于目标终点 destination，即：

• 从始点 source 到目标终点 destination 存在至少一条路径
• 如果存在从始点 source 到没有出边的节点的路径，则该节点就是路径终点。
• 从始点source到目标终点 destination 可能路径数是有限数字

当从始点 source 出发的所有路径都可以到达目标终点 destination 时返回 true，否则返回 false。

示例 1：

输入：n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
输出：false
说明：节点 1 和节点 2 都可以到达，但也会卡在那里。

示例 2：

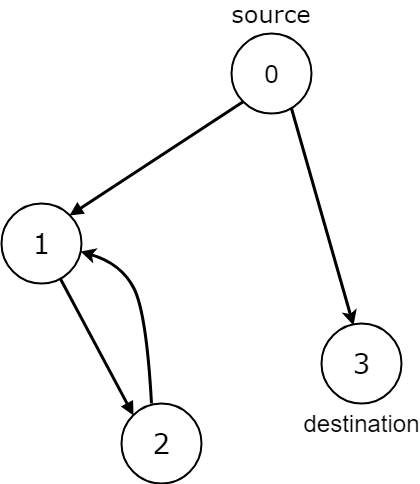
输入：n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
输出：false
说明：有两种可能：在节点 3 处结束，或是在节点 1 和节点 2 之间无限循环。

示例 3：

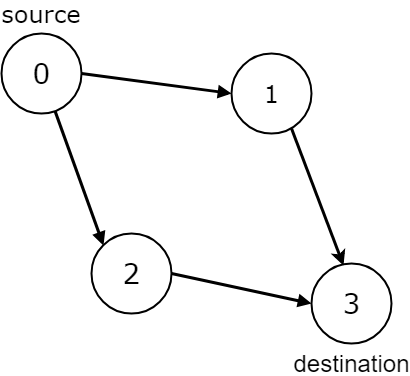
输入：n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
输出：true

示例 4：

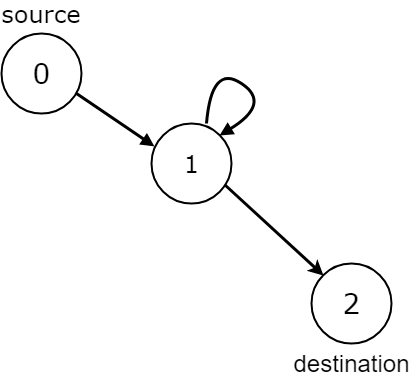
输入：n = 3, edges = [[0,1],[1,1],[1,2]], source = 0, destination = 2
输出：false
说明：从始点出发的所有路径都在目标终点结束，但存在无限多的路径，如 0-1-2，0-1-1-2，0-1-1-1-2，0-1-1-1-1-2 等。

示例 5：

输入：n = 2, edges = [[0,1],[1,1]], source = 0, destination = 1
输出：false
说明：在目标节点上存在无限的自环。

提示：

1. 给定的图中可能带有自环和平行边。
2. 图中的节点数 n 介于 1 和 10000 之间。
3. 图中的边数在 0 到 10000 之间。
4. 0 <= edges.length <= 10000
5. edges[i].length == 2
6. 0 <= source <= n - 1
7. 0 <= destination <= n - 1

---

764ms

class Solution {
    func leadsToDestination(_ n: Int, _ edges: [[Int]], _ source: Int, _ destination: Int) -> Bool {
        var graph:[Int:[Int]] = [Int:[Int]]()
        var path:Set<Int> = Set<Int>()
        var qu:[Int] = [Int]()
        for e in edges
        {
            graph[e[0],default:[Int]()].append(e[1])
        }
        if graph[destination] != nil
        {
            return false
        }
        if n == 1
        {
            return true
        }
        path.insert(source)
        if !dfs(&graph,&path,source,destination)
        {
            return false
        }
        return true 
    }
    
    func dfs(_ graph:inout [Int:[Int]],_ path:inout Set<Int>,_ last:Int,_ destination:Int) -> Bool
    {
        if graph[last] == nil
        {
            return false
        }
        for e in graph[last,default:[Int]()]
        {
            if path.contains(e)
            {
                return false
            }
            else
            {
                if e == destination
                {
                    continue
                }
                path.insert(e)
                if !dfs(&graph,&path,e,destination)
                {
                    return false
                }
                path.remove(e)
            }
        }
        return true        
    }
}