https://www.zhixincode.com/contest/7/problems
A题
分类讨论
当B有点需要经过时 穿梭的花费肯定为2*k,也可以发现,我们要找到包含所有需要经过的点(不含起点)的最小矩形,端点肯定是传送门,排序,找到需要经过最小的值和最大的值,再分别找小于等于和大于等于他们的传送门, 作为矩形端点,再判断起点的位置,最终得出答案。
当B无点需要经过时 分三种考虑,起点在最左边,最右边,在中间,很容易想到。
#include<bits/stdc++.h> #define all(a) (a).begin(),(a).end() using namespace std; typedef unsigned long long ull; const int maxn=2e6+10; int n,r,m,k,s; int main() { scanf("%d%d%d%d%d",&n,&r,&m,&k,&s); vector<int> x,y,zhuan{1,n}; for(int i=0;i<r;i++) { int a,b; scanf("%d%d",&a,&b); if(a==s&&b==0) continue; if(b==0) x.push_back(a); else y.push_back(a); } sort(all(x));sort(all(y)); while(m--) { int c; scanf("%d",&c); zhuan.push_back(c); } sort(all(zhuan)); if(y.size()>0) { int l,r; if(x.size()==0) r=*(--y.end()),l=*y.begin(); else { r=max(*(--x.end()),*(--y.end())); l=min(*x.begin(),*y.begin()); } int ans1=zhuan[upper_bound(all(zhuan),l)-zhuan.begin()-1]; int ans2=zhuan[lower_bound(all(zhuan),r)-zhuan.begin()]; int ans=(ans2-ans1+k)*2; if(s<ans1) ans+=(ans1-s)*2; else if(s>ans2) ans+=(s-ans2)*2; cout<<ans<<endl; return 0; } x.push_back(s); sort(all(x)); if(x.size()==1&&*x.begin()==s) cout<<0<<endl; else if(*x.begin()==s) { int ans=zhuan[lower_bound(all(zhuan),*(--x.end()))-zhuan.begin()]; cout<<(ans-s)*2<<endl; } else if(*(--x.end())==s) { int ans=zhuan[upper_bound(all(zhuan),*x.begin())-zhuan.begin()-1]; cout<<(s-ans)*2<<endl; } else { int ans1=zhuan[upper_bound(all(zhuan),*x.begin())-zhuan.begin()-1]; int ans2=zhuan[lower_bound(all(zhuan),*(--x.end()))-zhuan.begin()]; cout<<(ans2-ans1)*2<<endl; } } //20 4 2 50 4 //7 0 //13 0 //15 1 //6 1 //5 //15
B
dp dp[x][y][k]表示 第k秒 x,y 获得的最大值,初始化dp[xs][ys][0]=0其他数组为-inf 若干秒后 dp[x][y][k]>0 肯定是由起点转移过来的。
枚举时间找到满足的最小时间就好了。
#include<bits/stdc++.h> #define all(a) (a).begin(),(a).end() using namespace std; typedef unsigned long long ull; const int maxn=10200; int mp[20][20],dp[20][20][maxn]; int main() { int n,m,C,xs,xt,ys,yt; scanf("%d%d%d",&n,&m,&C); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&mp[i][j]); scanf("%d%d%d%d",&xs,&ys,&xt,&yt); memset(dp,-0x3f,sizeof(dp)); dp[xs][ys][0]=0; for(int k=1;k<maxn;k++) { for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { dp[i][j][k]=max({dp[i-1][j][k-1],dp[i][j+1][k-1],dp[i+1][j][k-1],dp[i][j-1][k-1],dp[i][j][k-1]})+(k%mp[i][j]==0?1:0); } } } int ans=-1; for(int i=0;i<maxn;i++) { if(dp[xt][yt][i]>=C) { ans=i; break; } } printf("%d ",ans); }
C 不会证,但是猜到了。。。
E
树形dp dp[x][0]表示不选x,dp[x][1]表示选择x,根据题意写状态转移方程就好了
#include <bits/stdc++.h> #define pb push_back #define mp make_pair #define fi first #define se second #define all(a) (a).begin(), (a).end() #define fillchar(a, x) memset(a, x, sizeof(a)) #define huan printf(" ") #define debug(a,b) cout<<a<<" "<<b<<" "<<endl #define ffread(a) fastIO::read(a) using namespace std; typedef long long ll; const int maxn = 1e5+10; const int maxm = 1e4+10; const int inf = 0x3f3f3f3f; const ll mod = 998244353; const double epx = 1e-6; const double pi = acos(-1.0); //head------------------------------------------------------------------ struct edge { int to,next; }e[maxn]; int head[maxn],tot; int dp[maxn][2],vis[maxn],f[maxn],d[maxn],n; void init() { tot=0; fillchar(head,-1); fillchar(vis,0); } void add(int u,int v) { e[tot].to=v; e[tot].next=head[u]; head[u]=tot++; } void dfs(int x,int y) { vis[x]=1; dp[x][0]=0; dp[x][1]=f[x]; for(int i=head[x];i!=-1;i=e[i].next) { int v=e[i].to; if(v==y) continue; dfs(v,x); dp[x][0]+=max(dp[v][0],dp[v][1]); dp[x][1]+=max(dp[v][0],dp[v][1]-d[min(x,v)]); } } int main() { init(); cin>>n; for(int i=1;i<=n;i++) cin>>f[i]; for(int i=1;i<=n;i++) cin>>d[i]; for(int i=2;i<=n;i++) { if(i%2==0) add(i/2,i),add(i,i/2); else if(3*i+1<=n) add(3*i+1,i),add(i,3*i+1); } int ans=0; for(int i=1;i<=n;i++) if(!vis[i]) { dfs(i,-1); ans+=max(dp[i][1],dp[i][0]); } cout<<ans<<endl; }
F最短路
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<bitset> #include<cassert> #include<cctype> #include<cmath> #include<cstdlib> #include<ctime> #include<deque> #include<iomanip> #include<list> #include<map> #include<queue> #include<set> #include<stack> #include<vector> using namespace std; typedef long long ll; typedef long double ld; typedef pair<int,int> pii; const double PI=acos(-1.0); const double eps=1e-6; const ll mod=1e9+7; const int inf=0x3f3f3f3f; const int maxn=1e5+10; const int maxm=100+10; #define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); int n,m,k; int cnt=0,head[maxn<<2]; bool vist[maxn]; ll dis[maxn],body[maxn]; priority_queue<pair<ll,int>,vector<pair<ll,int> >,greater<pair<ll,int> > >q; struct node{ int v,nex; ll w; }edge[maxn<<2]; void add(int u,int v,ll w) { edge[cnt].v=v; edge[cnt].w=w; edge[cnt].nex=head[u]; head[u]=cnt++; } void dijkstra(int s) { dis[s]=0;//到自己的最短距离直接设为0 q.push(make_pair(0,s)); while(!q.empty()){//队列非空 int u=q.top().second;q.pop(); vist[u]=true; for(int i=head[u];~i;i=edge[i].nex){ int v=edge[i].v; ll w=edge[i].w+(body[v]>k?(body[v]-k)*(body[v]-k):0); if(dis[v]>dis[u]+w){//满足条件更新距离 dis[v]=dis[u]+w; //p[v]=u;//保存路径 q.push(make_pair(dis[v],v));//把更新完的值压入队列 } } } } int main() { memset(head,-1,sizeof(head));//初始化数组 memset(vist,false,sizeof(vist)); //memset(dis,inf,sizeof(dis)); cin>>n>>m>>k; for(int i=0;i<=n;i++) dis[i]=1e18; for(int i=1;i<=n;i++) cin>>body[i]; for(int i=1;i<=m;i++){ int u,v;ll w; cin>>u>>v>>w; add(u,v,w); add(v,u,w);//无向图相互可达 有向图一次就好 } k+=body[1]; dijkstra(1); cout<<dis[n]<<endl;
I 树状数组+dfs
解析 长度肯定是奇数3,5,7,9...然后会发现 长度5的是两个长度3的连起来,长度7的是三个长度3的连起来...
那我们就先来找长度为3的序列 枚举左右端点l r, 由于每个数的大小不超过2000,所以我们开2000个树状数组来记录小于j的个数
所以就有 if(a[l]>a[r]) 我们getsum(a[r],r)-getsum(a[r],l)得到(l,r) 区间中小于a[r]的个数k,然后 l - ->r 连一条有向边权值为k
复杂度O(n*n*log(n))
图建完之后dfs计数dp[i] 表示以i为起点的路径总数 从叶子向上递归。
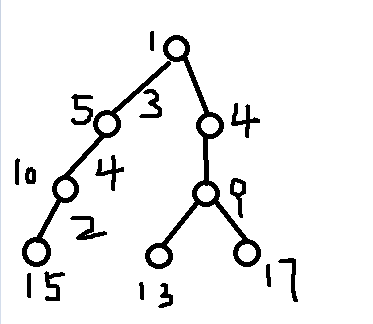
1-->5-->10-->15 这条链的过程就是 dp[15]=0,dp[10]=dp[15]*2+2,dp[5]=dp[10]*4+4,dp[1]=dp[5]*3+3
枚举起点,采用记忆化来降低复杂度,O(n)。
这个解法不是最好的,其他大佬代码又短又快QAQ。
#include <bits/stdc++.h> #define pb push_back #define mp make_pair #define fi first #define se second #define all(a) (a).begin(), (a).end() #define fillchar(a, x) memset(a, x, sizeof(a)) #define huan printf(" ") #define debug(a,b) cout<<a<<" "<<b<<" "<<endl #define ffread(a) fastIO::read(a) using namespace std; typedef long long ll; const int maxn = 2e3+10; const int inf = 0x3f3f3f3f; const ll mod = 1000000007; const double epx = 1e-6; const double pi = acos(-1.0); //head------------------------------------------------------------------ int a[maxn],c[maxn][maxn],tot,n,head[maxn],vis[maxn]; ll dp[maxn]; //对应原数组和树状数组 int lowbit(int x){ return x&(-x); } void updata(int j,int i,int k) { while(i <= n){ c[j][i] += k; i += lowbit(i); } } int getsum(int j,int i) { //求A[1 - i]的和 int res = 0; while(i > 0){ res += c[j][i]; i -= lowbit(i); } return res; } struct edge { int to,val,next; }e[maxn*maxn]; void add(int u,int v,int w) { e[tot].val=w; e[tot].to=v; e[tot].next=head[u]; head[u]=tot++; } void init() { tot=0; memset(head,-1,sizeof(head)); memset(vis,0,sizeof(vis)); } void dfs(int x) { if(vis[x]) return; for(int i=head[x];i!=-1;i=e[i].next) { ll v=e[i].to,w=e[i].val; dfs(v); dp[x]=(dp[x]+dp[v]*w%mod+w)%mod; } vis[x]=1; } int main() { init(); //freopen("C:\Users\HP\Desktop\a.txt","r",stdin); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); for(int j=a[i]+1;j<=n;j++) updata(j,i,1); } for(int i=1;i<=n;i++) { for(int j=i+2;j<=n;j++) { if(a[i]<a[j])continue; int temp=getsum(a[j],j)-getsum(a[j],i); if(temp) add(a[i],a[j],temp); } } ll ans=0; for(int i=1;i<=n;i++) { dfs(a[i]); ans=(ans+dp[a[i]])%mod; } printf("%lld ",ans); }
J 这题应该是cf原题了 做法是枚举答案。