【洛谷P5904】HOT-Hotels 加强版

题目

题目链接：https://www.luogu.com.cn/problem/P5904
给出一棵有 (n) 个点的树，求有多少组点 ((i,j,k)) 满足 (i,j,k) 两两之间的距离都相等。
((i,j,k)) 与 ((i,k,j)) 算作同一组。
(nleq 10^5)。

思路

本代码也可以通过原题。
考虑到三元组只有可能是以下三种情况，所以考虑 dp。

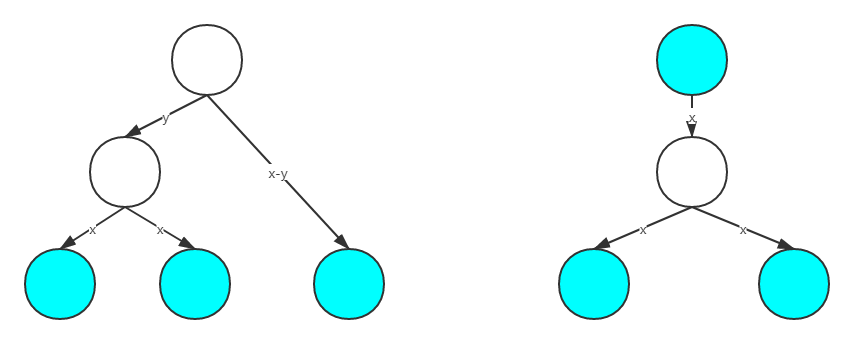
设 (f_{i,j}) 表示在 (i) 子树内， 与 (i) 距离为 (j) 的节点的数量，(g_{i,j}) 表示在 (i) 子树内，(mathrm{dis}(x,mathrm{lca}(x,y))=mathrm{dis}(y,mathrm{lca}(x,y))=mathrm{dis}(i,mathrm{lca}(x,y))+j) 的二元组 ((i,j)) 数量。
考虑加入 (x) 的一棵子树 (y)，对答案的贡献为

[sum^{mathrm{maxd}(y)-1}_{i=1}f_{x,i-1} imes g_{y,i}+sum^{mathrm{maxd}(y)-1}_{i=0}g_{x,i} imes f_{y,i+1} ]

注意还需要加上特殊情况 (g_{x,0})。
然后考虑 (g) 的转移，有

[g_{x,i+1}gets f_{x,i} imes f_{y,i-1} ]

[g_{x,i}gets g_{y,i+1} ]

最后 (f) 的转移很简单

[f_{x,i}gets f_{y,i-1} ]

这样转移就完成了。直接做是 (O(n^2)) 的，可以过原题。
发现转移都与深度有关，所以可以用长剖优化。
注意 (g) 的转移时，(g[son[x]]) 所占的内存应该是 (g[x]) 往左一位，所以必须开二倍空间，并且每一个长链顶端的内存要与上一个长链空出一倍。请务必理解这句话。
时间复杂度 (O(n))。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N=100010;
int n,tot,maxd[N],son[N],head[N];
ll kel[N],fad[N*2],*f[N],*g[N*2],*nowf=kel,*nowg=fad;
ll ans;

struct edge
{
	int next,to;
}e[N*2];

void add(int from,int to)
{
	e[++tot]=(edge){head[from],to};
	head[from]=tot;
}

void dfs1(int x,int fa)
{
	for (int i=head[x];~i;i=e[i].next)
	{
		int v=e[i].to;
		if (v!=fa)
		{
			dfs1(v,x);
			if (maxd[v]>maxd[son[x]]) son[x]=v;
		}
	}
	maxd[x]=maxd[son[x]]+1;
}

void dfs2(int x,int fa)
{
	f[x][0]=1;
	if (son[x])
	{
		f[son[x]]=f[x]+1;
		g[son[x]]=g[x]-1;
		dfs2(son[x],x);
	}
	ans+=g[x][0];
	for (int i=head[x];~i;i=e[i].next)
	{
		int v=e[i].to;
		if (v!=fa && v!=son[x])
		{
			f[v]=nowf; nowf+=maxd[v];
			g[v]=nowg+maxd[v]; nowg+=maxd[v]*2;
			dfs2(v,x);
			for (int i=1;i<maxd[v];i++)
				ans+=f[x][i-1]*g[v][i];
			for (int i=0;i<maxd[v];i++)
				ans+=f[v][i]*g[x][i+1];	
			for (int i=0;i<maxd[v];i++)
				g[x][i+1]+=f[x][i+1]*f[v][i];
			for (int i=1;i<maxd[v];i++)
				g[x][i-1]+=g[v][i];
			for (int i=0;i<maxd[v];i++)
				f[x][i+1]+=f[v][i];
		}
	}
}

int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d",&n);
	for (int i=1,x,y;i<n;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y); add(y,x);
	}
	dfs1(1,0);
	f[1]=nowf; nowf+=maxd[1];
	g[1]=nowg+maxd[1]; nowg+=2*maxd[1];
	dfs2(1,0);
	printf("%lld",ans);
	return 0;
}