【洛谷P4294】游览计划

题目

题目链接：https://www.luogu.com.cn/problem/P4294
从未来过绍兴的小D有幸参加了Winter Camp 2008，他被这座历史名城的秀丽风景所吸引，强烈要求游览绍兴及其周边的所有景点。
主办者将绍兴划分为N行M列(N×M)个分块，如下图(8×8)：

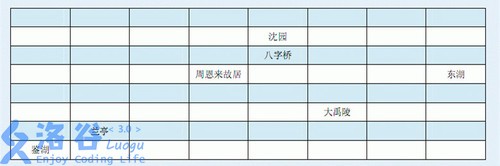
景点含于方块内，且一个方块至多有一个景点。无景点的方块视为路。
为了保证安全与便利，主办方依据路况和治安状况，在非景点的一些方块内安排不同数量的志愿者；在景点内聘请导游（导游不是志愿者）。在选择旅游方案时，保证任意两个景点之间，存在一条路径，在这条路径所经过的每一个方块都有志愿者或者该方块为景点。既能满足选手们游览的需要，又能够让志愿者的总数最少。
例如，在上面的例子中，在每个没有景点的方块中填入一个数字，表示控制该方块最少需要的志愿者数目：

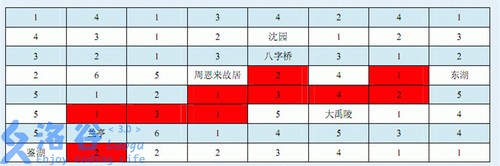
图中用深色标出的方块区域就是一种可行的志愿者安排方案，一共需要20名志愿者。由图可见，两个相邻的景点是直接（有景点内的路）连通的（如沈园和八字桥）。
现在，希望你能够帮助主办方找到一种最好的安排方案。

思路

斯坦纳树模板题。
斯坦纳树是这样一类问题：一张无向图，有\(k\)个特殊点，选择若干权值和最小的路径使得特殊点两两连通。
需要使用到状压，所以这类问题一般\(k\)很小，而又要枚举所有的点，所以\(n\)也一般较小。
首先显然这最终会是一棵树。
设\(f[i][s]\)表示以\(i\)为根的树，将集合\(s\)里所有点都联通的最小代价。
那么有

\[f[i][s]=\min_{k\in s} f[i][k]+f[i][s\ \operatorname{xor}\ k]-cost[i] \]

这是针对将两个以\(i\)为根的子树合并的情况。对于从点\(j\)转移到点\(i\)的情况，有

\[f[i][s]=f[j][s]+cost[i] \]

而这个方程是无序的，而我们又要求最小，所以可以在 SPFA 的过程中进行转移。
这就是模板斯坦纳树的做法。

回到本题，显然我们只需要把模板中的无向图变成网格即可。设\(f[x][y][s]\)表示以\((x,y)\)为根，选择特殊点集合\(s\)的点所需最小代价。转移同理。
至于输出路径，我们设\(pre[x][y][s]\)表示是从哪一个状态转移到\(f[x][y][s]\)的，dfs 寻找路径即可。
时间复杂度\(O(nm·4^k)\)，远远跑不满。

代码

#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=15,S=1030,Inf=1e9;
const int dx[]={0,0,0,-1,1};
const int dy[]={0,-1,1,0,0};
int n,m,rtx,rty,cnt,a[N][N],f[N][N][S];
bool vis[N][N];
char ans[N][N];

struct node
{
	int x,y,s;
}pre[N][N][S];

queue<node> q;

void spfa(int S)
{
	while (q.size())
	{
		node u=q.front();
		q.pop();
		vis[u.x][u.y]=0;
		for (int i=1;i<=4;i++)
		{
			int x=u.x+dx[i],y=u.y+dy[i];
			if (x<1 || x>n || y<1 || y>m) continue;
			if (f[x][y][S]>f[u.x][u.y][S]+a[x][y])
			{
				f[x][y][S]=f[u.x][u.y][S]+a[x][y];
				pre[x][y][S]=u;
				if (!vis[x][y])
				{
					vis[x][y]=1;
					q.push((node){x,y,S});
				}
			}
		}
	}
}

void dfs(int x,int y,int s)
{
	if (!pre[x][y][s].s) return;
	if (ans[x][y]!='x') ans[x][y]='o';
	dfs(pre[x][y][s].x,pre[x][y][s].y,pre[x][y][s].s);
	if (pre[x][y][s].x==x && pre[x][y][s].y==y)
		dfs(x,y,s^pre[x][y][s].s);
}

int main()
{
	memset(f,0x3f3f3f3f,sizeof(f));
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
		{
			ans[i][j]='_';
			f[i][j][0]=0;
			scanf("%d",&a[i][j]);
			if (!a[i][j])
			{
				cnt++;
				ans[i][j]='x';
				f[i][j][1<<cnt-1]=0;
				rtx=i; rty=j;
			}
		}
	for (int s=1;s<(1<<cnt);s++)
	{
		memset(vis,0,sizeof(vis));
		while (q.size()) q.pop();
		for (int i=1;i<=n;i++)
			for (int j=1;j<=m;j++)
			{
				for (int k=s;k;k=s&(k-1))
					if (f[i][j][s]>f[i][j][k]+f[i][j][s^k]-a[i][j])
					{
						f[i][j][s]=f[i][j][k]+f[i][j][s^k]-a[i][j];
						pre[i][j][s]=(node){i,j,k};
					}
				if (f[i][j][s]<Inf)
				{
					q.push((node){i,j,s});
					vis[i][j]=1;
				}
			}
		spfa(s);
	}
	dfs(rtx,rty,(1<<cnt)-1);
	printf("%d\n",f[rtx][rty][(1<<cnt)-1]);
	for (int i=1;i<=n;i++)
		printf("%s\n",ans[i]+1);
	return 0;
}