【CF297E】Mystic Carvings

\(\rm Update\ on\ 2020.02.11\)：在CF的题库中A了这道题，将标题和题目链接更改。

题目

题目链接：https://www.luogu.com.cn/problem/CF297E
一个环上有标号为\(1\)到\(2n\)的顶点，每个顶点连接一条无向边。要求选择\(3\)条不重复的边在顶点处建熊洞（共\(6\)个），且每条边的两个顶点的距离相同，询问其方案数。
距离定义为在环上从一个顶点到另一个顶点所经过的最少熊洞数量-1。

思路

\(3\)条弦在一个圆中的相交情况只有如下五种：

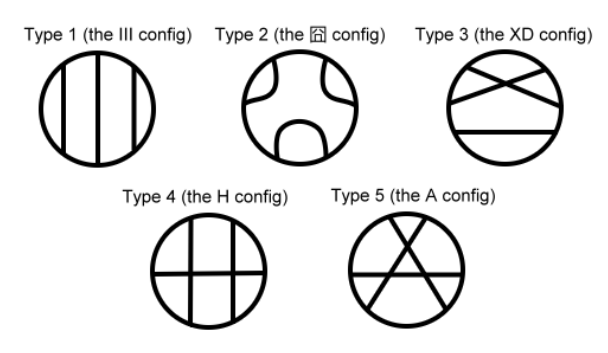
我们发现，满足题目要求的只有2号和5号。而这两种图形的方案都不是很好计算，所以考虑计算出不满足题目条件的图形个数。
假设我们先求出了\(l[i],r[i]\)表示第\(i\)条弦的左右分别有多少条与它不相交的弦，那么图1的情况就有\(\sum^{n}_{i=1}l[i]\times r[i]\)种，而图3和图4都有共同点：3条弦中都有两条弦满足另外两条线分别于它相交和相离，所以方案数就是\(\frac{(l[i]+r[i])\times (n-l[i]-r[i]-1)}{2}\).
那么现在的问题就是如何求\(l[i],r[i]\)，容易发现，一条弦在另一条弦的左/右边，其实就是判断这两条线所连接的点的大小，分类讨论+二维偏序即可。
时间复杂度\(O(n\log n)\)

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;

const int N=300010;
int n,l[N],r[N];
ll ans1,ans2;

struct node
{
	int x,y,id;
}a[N];

struct BIT
{
	int c[N];
	
	void add(int x,int val)
	{
		for (;x<=n*2;x+=x&-x)
			c[x]+=val;
	}
	
	int ask(int x)
	{
		int sum=0;
		for (;x;x-=x&-x)
			sum+=c[x];
		return sum;
	}
}bit;

bool cmp1(node x,node y)
{
	return x.x<y.x;
}

bool cmp2(node x,node y)
{
	return x.y>y.y;
}

int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i].x,&a[i].y);
		if (a[i].x>a[i].y) swap(a[i].x,a[i].y);
		a[i].id=i;
	}
	sort(a+1,a+1+n,cmp1);
	for (int i=1;i<=n;i++)
	{
		l[a[i].id]+=bit.ask(a[i].x)+bit.ask(n*2)-bit.ask(a[i].y);
		bit.add(a[i].y,1);
	}
	memset(bit.c,0,sizeof(bit.c));
	for (int i=n;i>=1;i--)
	{
		r[a[i].id]+=bit.ask(a[i].y)-bit.ask(a[i].x);
		bit.add(a[i].y,1);
	}
	memset(bit.c,0,sizeof(bit.c));
	sort(a+1,a+1+n,cmp2);
	for (int i=1;i<=n;i++)
	{
		l[a[i].id]+=bit.ask(n*2)-bit.ask(a[i].y);
		bit.add(a[i].x,1);
	}
	ans1=1LL*n*(n-1)*(n-2)/6;
	for (int i=1;i<=n;i++)
	{
		ans1-=1LL*l[i]*r[i];
		ans2+=1LL*(l[i]+r[i])*(n-l[i]-r[i]-1);
	}
	printf("%I64d",ans1-ans2/2);
	return 0;
}