暑假D4T3 construct ([SHOI2010]最小生成树)

题目描述

钦定一条边，使得他一定在最小生成树中，一种操作：选定一条边，讲除他之外的边边权+1，求最少操作次数

题解

正解网络流，不过我太菜了，想不到。

这道题晃一眼以为和次小生成树差不多，于是考虑先用kruskal求一遍最小生成树，建出树来，再在环上找最大的边，让他增加。

不过仔细思考一下就发现有问题，比如

 

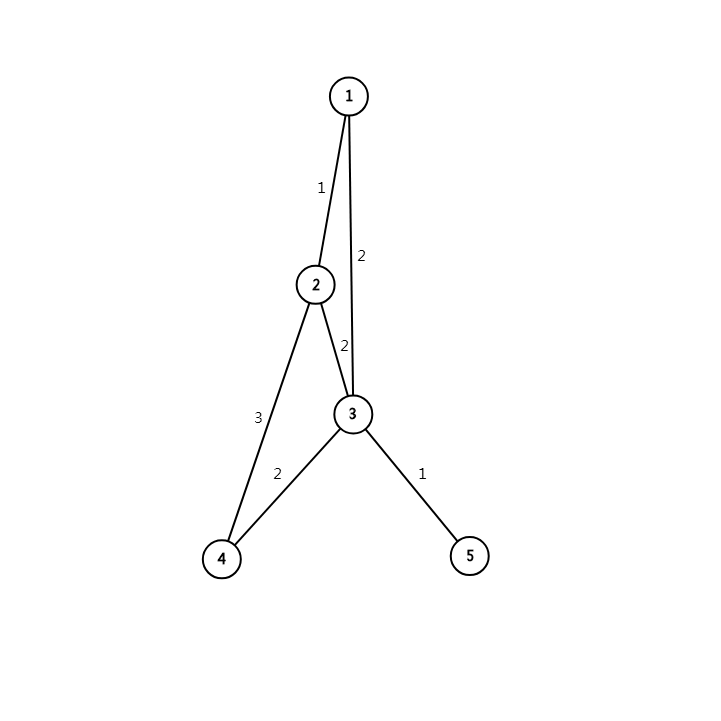
这颗最小生成树可能是(1,2,1),(2,3,2),(3,4,2),(3,5,1) 我们需要将(2,4,3)这条边放进去，那么按照次小生成树的做法，你可能断的是(2,3,2)这条边，但是你会发现你还是不能选你想选的边，因为(1,3,2)更优。

思考为什么会这样？

可以知道，在最小生成树上断开一条边，可以得到两个联通块，所有可以连接这两个联通块的且边权小的边对答案是有贡献的。

所以我们考虑枚举环上所以的边，断开，然后在加上边权小的贡献，每次得到的答案取min即可。

我们怎么满足一定会被选这个条件呢，所以我们做kruskal时要尽量不选他，这个条件只是在选择边权相同的边时有影响，所以我们只需要在给要选的边另一个权值，在排序时边权为第一关键字，新权值为第二关键字就OK了。其实或许排序里面判断编号也可以。

我们在最初kruskal时将选过的边打个标记，在dfs建树时将边的编号给儿子，在枚举断边时按照暴力的找lca的方法即可，将记录的编号id传入nice函数（求断这边的答案），用打了标记的边做kruskal，除了编号为id的边，这样就达到了断开这条边的目的。最后再扫一遍需要放进去的边之前的边，如果这条边能够连接两个联通块，就记录他的贡献。 至于为什么时间复杂度可以过，可以看到n，m都很小，排序是O(mlogm),对于最后求答案O(m(m*x))，x是一次并查集的复杂度，其实我也不知道，反正能过，总共也32ms

#include<bits/stdc++.h>
using namespace std;

const int maxn=505;
const int maxm=805;
int n,m,cnt,end;
int k,xx,yy,vv,ans;
bool opt;
int fa[maxn];
int dep[maxn],anc[maxn],w[maxn];
struct edge{
    int x,y,id,val,cx;
    bool used;
}e[maxm];
vector<pair<int,int> >a[maxn];


template<class T>inline void read(T &x){
    x=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
}

bool cmp(edge a,edge b){
    if(a.val==b.val) return a.cx<b.cx;
    return a.val<b.val;
}

int find(int x){
    if(fa[x]==x) return x;
    return fa[x]=find(fa[x]);
}

void dfs(int u){
    for(unsigned int i=0;i<a[u].size();i++){
        int v=a[u][i].first;
        if(v==anc[u]) continue;
        dep[v]=dep[u]+1;
        w[v]=a[u][i].second;
        anc[v]=u;
        dfs(v);
    }
}

int nice(int id){
    int ret=0;
    for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=1;i<=end;i++){
        if(e[i].id==id){continue;}
        if(e[i].used) fa[find(e[i].x)]=find(e[i].y);
    }
    for(int i=1;e[i].id!=k;i++){
        int dx=find(e[i].x),dy=find(e[i].y);
        if(dx!=dy){
            ret+=vv-e[i].val+1;
        }
    }
    return ret;
}

void work(int x,int y){
    ans=500000000;
    if(dep[x]>dep[y]) swap(x,y);
    while(dep[x]!=dep[y]){
        ans=min(ans,nice(w[y]));
        y=anc[y];
    }
    while(x!=y){
        ans=min(ans,nice(w[y]));
        ans=min(ans,nice(w[x]));
        x=anc[x];y=anc[y];
    }
}

int main(){
    //freopen("construct.in","r",stdin);
    //freopen("construct.out","w",stdout);
    read(n);read(m);read(k);
    for(int i=1;i<=m;i++){
        read(e[i].x);read(e[i].y);read(e[i].val);
        e[i].id=i;
        fa[i]=i;
    }
    e[k].cx=0x3f3f3f;
    xx=e[k].x;yy=e[k].y;
    vv=e[k].val;
    sort(e+1,e+m+1,cmp);
    int p=0;
    for(int i=1;i<=m;i++){
        int dx=find(e[i].x),dy=find(e[i].y);
        if(dx!=dy){
            fa[dx]=dy;
            a[e[i].x].push_back(make_pair(e[i].y,e[i].id));
            a[e[i].y].push_back(make_pair(e[i].x,e[i].id));
            e[i].used=true;
            if(e[i].id==k) opt=true;
            p++;
        }
        if(p==n-1) {end=i;break;}
    }
    if(opt) {printf("0");return 0;}
    dep[1]=1;
    memset(anc,0,sizeof(anc));
    dfs(1);
    work(xx,yy);
    printf("%d",ans);
}
/*
5 6 1
2 4 3
1 2 1
1 3 2
2 3 2
3 4 2
3 5 1
*/