通用数据结构关系
可以根据下图选择合适的通用数据结构
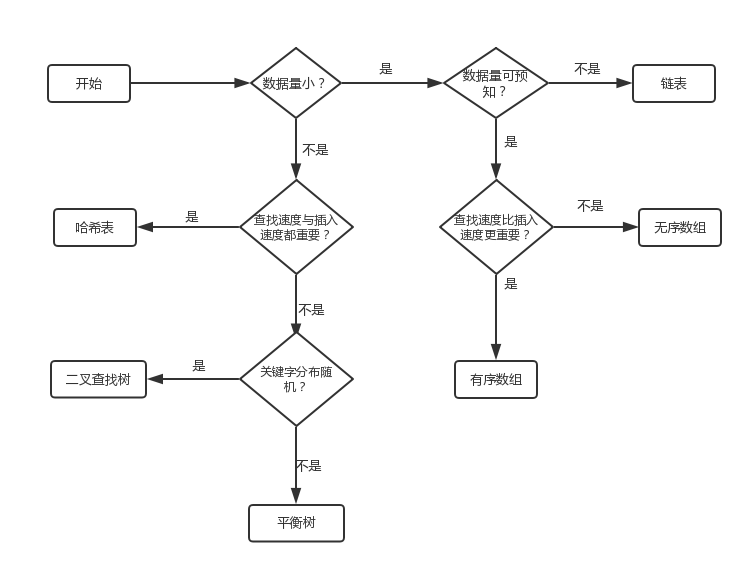
数组
使用场景
数组在以下三个情形下很有用:
1)数据量较小。
2)数据规模已知。
3)随机访问,修改元素值。
如果插入速度很重要,选择无序数组。如果查找速度很重要,选择有序数组,并使用二分查找。
缺点
1)需要预先知道数据规模
2)插入效率低,因为需要移动大量元素。
链表
解决的问题
链表的出现解决了数组的两个问题:
1)需要预先知道数据规模
2)插入效率低
使用场景
1)数据量较小
2)不需要预先知道数据规模
3)适应于频繁的插入操作
缺点
1)有序数组可以通过二分查找方法具有很高的查找效率(O(log n)),而链表只能使用顺序查找,效率低下(O(n))。
二叉搜索树
解决的问题
1)有序数组具有较高的查找效率(O(log n)),而链表具有较高的插入效率(头插法,O(1)),结合这两种数据结构,创建一种貌似完美的数据结构,也就是二叉搜索树。
使用场景
1)数据是随机分布的
2)数据量较大
3)频繁的查找和插入操作(可以提供O(log n)级的查找、插入和删除操作)
缺点
1)如果处理的数据是有序的(升序/降序),那么构造的二叉搜索树就会只有左子树(或右子树),也就是退化为链表,查找效率低下(O(log n))。
平衡树
解决的问题
1)针对二叉搜索树可能会退化为链表的情况,提出了平衡树,平衡树要求任意节点的左右两个子树的高度差不超过1,避免退化为链表的情况。
使用场景
1)无论数据分布是否随机都可以提供O(log n)级别的查找、插入和删除效率
2)数据量较大
缺点
1)平衡树的实现过于复杂。
哈希表
解决的问题
同平衡树一样,哈希表也不要求数据分布是否随机,不过哈希表的实现比平衡树要简单得多。
使用场景
1)不需要对最大最小值存取。
2)无论数据分布是否随机,理想情况下(无冲突)可以提供O(1)级别的插入、查找和删除效率。
3)数据量较大
缺点
1)由于是基于数组的,数组(哈希表)创建后难以扩展,使用开放地址法的哈希表在基本被填满时,性能下降的非常严重。
2)不能对最大最小值存取。