看来我果然还是太菜,只能看看思路才能AC
-
题意
自己查...
-
solution
设dp[x]为从x到t最小需要控制次数
对于一个点,我们有两种选择:控制,或者不控制
基于这个,dp方程或许很好推: (dp[now]=min(max{dp[to]},min{dp[to]}+1)) to为从x点所能到达的所有点
那么问题来了,怎么更新dp值?
因为图很复杂,你用来更新其他点的点,可能又会被其他点更新(即有其他策略),
所以我们要采用一种类似spfa的方法,把更新过的点推进队列.
如何更新:对于一个点,我们用它的值来更新原图上能直接到达它的点的min{dp[to]}+1,然后用原图上它能到达的点的值来更新它的max{dp[to]}
而且我们要从t倒着搜到s,所以我们要建个反向图跑spfa
但是还有一个问题,我们不能让机器人boom掉
其实这个不难,因为机器人不走回路肯定比走回路优,所以dp避免了boom的情况
贴个图理解一下
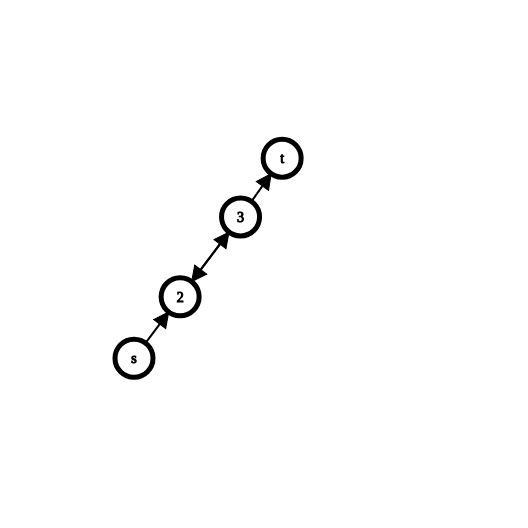
我们在t这一点用dpt来更新dp[3]使dp[3]=1(min{dp[to]}+1)
在3这一点用dp[3]来更新dp[2]使dp[2]=2(min{dp[to]}+1)
同在3这一点,我们发现此时max{dp[to]}=dp[2]=2,不能更新dp[3]
但在2这一点,max{dp[to]}=dp[3]=1,把dp[2]更新成2
dp更新的流程就是这样.
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>
#define N 1000005
using namespace std;
vector<int> G[N],G2[N];
int f[N];
bool vis[N];
int n,m,s,t;
queue<int> q;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
G[a].push_back(b);
G2[b].push_back(a);
}
scanf("%d%d",&s,&t);
memset(f,0X3f,sizeof f);
memset(vis,false,sizeof vis);
q.push(t);
f[t]=0;
vis[t]=1;
while(!q.empty()){
int now=q.front();
q.pop();
vis[now]=0;
for(int i=0;i<G2[now].size();i++){
int to=G2[now][i];
if(f[to]>f[now]+1){
f[to]=f[now]+1;
if(!vis[to]){
vis[to]=true;
q.push(to);
}
}
}
int plk=0;
for(int i=0;i<G[now].size();i++)plk=max(plk,f[G[now][i]]);
if(plk<f[now]){
f[now]=plk;
if(!vis[now]){
vis[now]=true;
q.push(now);
}
}
}
if(f[s]==0X3f3f3f3f)cout<<-1;
else cout<<f[s];
}
