-
题意
给你一个点集,你需要画两条直线,它们一条和y=-x平行,一条和y=x平行
目标是让这个每个到直线(距离较小的一条)的曼哈顿距离的最大值最小
-
solution
坐标轴旋转+二分
因为直线斜率固定,所以曼哈顿距离等于(sqrt{2})倍
我的做法是让点集绕原点旋转45°并且放大(sqrt{2})倍,变换方法是(x,y)->(x-y,x+y)还同时使变换后的坐标为整数便于二分
这时你需要画的十字架是和x轴,轴分别平行的,而且点到直线的距离就是其横坐标/纵坐标
然后二分最大距离
举例,check时可行的点(与直线的距离小于等于二分值)构成了一个这样的图形
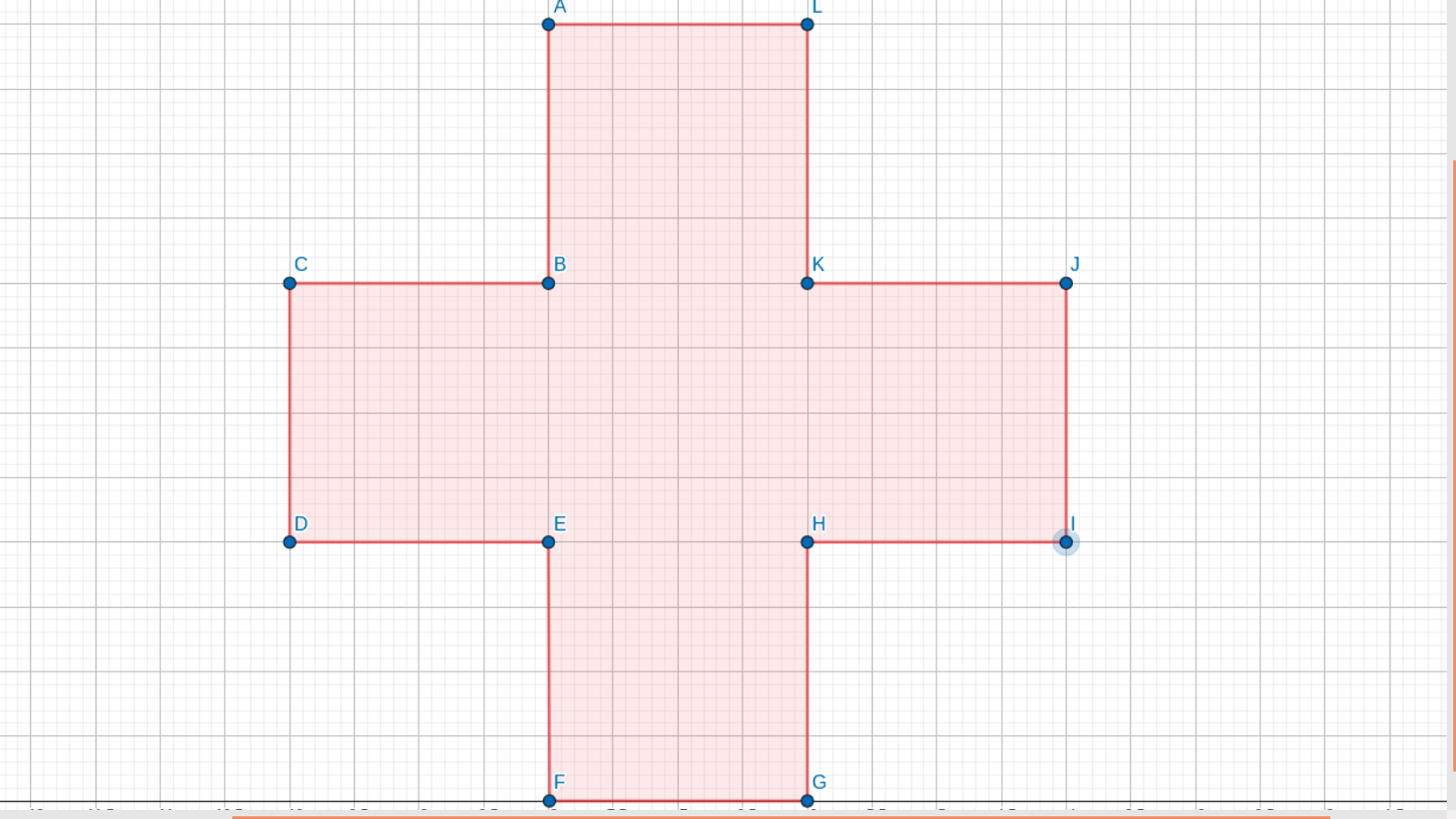
把它分成横着的和竖着的长方形
那么我们用竖着的长方形横向覆盖
然后O(n)预处理左右两端的最高点和最低点,以便判断是否能用横向的长方形覆盖
如上
-
code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define int long long
#define N 200005
using namespace std;
int n;
const double eps=1e-6;
struct sett{
int x,y;
bool operator<(const sett& a)const{
return (x^a.x)?(x<a.x):(y<a.y);
}
}lib[N];
int left_up[N],left_down[N];
int right_up[N],right_down[N];
bool check(int k){
int fr=1,la=1;
for(;fr<=n;fr++){
for(;la<=n&&lib[fr].x+k>=lib[la].x;la++);
la--;
if(max(left_up[fr-1],right_up[la+1])-min(left_down[fr-1],right_down[la+1])<=k)return true;
}
return false;
}
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
int x,y;
scanf("%lld%lld",&x,&y);
lib[i]=(sett){x-y,x+y};
}
sort(lib+1,lib+n+1);
left_up[0]=right_up[n+1]=-2e10;
left_down[0]=right_down[n+1]=2e10;
for(int i=1;i<=n;i++){
left_up[i]=max(left_up[i-1],lib[i].y);
left_down[i]=min(left_down[i-1],lib[i].y);
}
for(int i=n;i>=1;i--){
right_up[i]=max(right_up[i+1],lib[i].y);
right_down[i]=min(right_down[i+1],lib[i].y);
}
int l=0,r=1e10,mid;
while(r>l){
mid=(l+r)/2;
if(check(mid))r=mid;
else l=mid+1;
}
printf("%.6lf",(double)(r/2.0));
}