576. 出界的路径数 力扣（中等） 路径dp/记忆化搜索 都不会做

576. 出界的路径数

给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你 最多 可以移动 maxMove 次球。

给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余 后的结果。

示例 1：

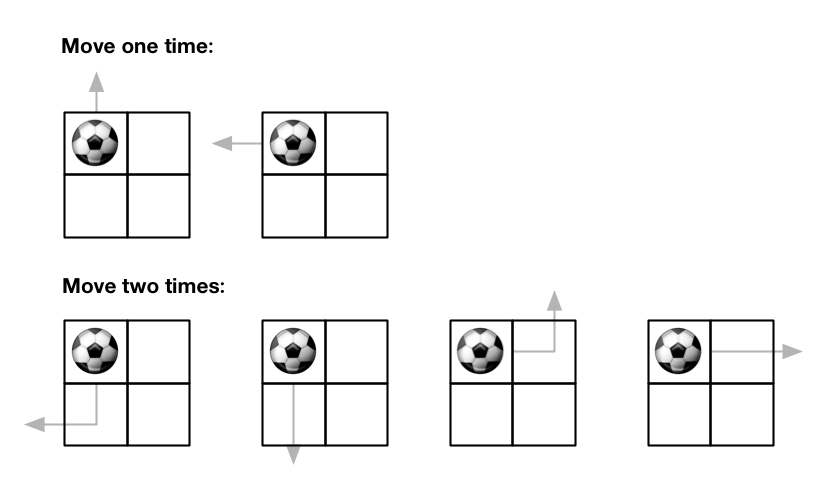
输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
输出：6

题解：

动态规划：https://leetcode-cn.com/problems/out-of-boundary-paths/solution/chu-jie-de-lu-jing-shu-by-leetcode-solut-l9dw/

如果dp不好入手的情况，可以先写个记忆化搜索版本

记忆化搜索：

https://leetcode-cn.com/problems/out-of-boundary-paths/solution/gong-shui-san-xie-yi-ti-shuang-jie-ji-yi-asrz/

https://leetcode-cn.com/problems/out-of-boundary-paths/solution/576-chu-jie-de-lu-jing-shu-ji-yi-hua-sou-7sg4/

https://leetcode-cn.com/problems/out-of-boundary-paths/solution/yi-ti-wu-jie-dfs-jian-zhi-ji-yi-hua-sou-k4dtg/

代码：

动态规划写法：

// 想到了动态规划，dp[i][j][k]到位置（i,j）走了k步的方法数
// 甚至对状态转移方程有了一点想法，但是问题是：起始点不是(0,0)就想不通了，这样也可以进行动态规划吗？？
// 结果记忆化搜索，我吐了呀……

//  执行用时：80 ms，内存消耗：16.5 MB
class Solution {
public:
    int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
    
     vector<vector<int>> dr={{1,0},{0,1},{-1,0},{0,-1}};
     int mod=1e9+7,res=0;
     int dp[55][55][55];
     memset(dp,0,sizeof(dp));
     dp[0][startRow][startColumn]=1;       // 起始状态标记 
     for(int move=0;move<maxMove;move++)   // 控制步数不超过maxMove
     {
         for(int i=0;i<m;i++)
            for(int j=0;j<n;j++)
             if(dp[move][i][j]>0)
            {
                for(auto d:dr)
                {
                    int x=i+d[0];
                    int y=j+d[1];
                    if ( (x<0 || x>=m) || (y<0 || y>=n) ) res=(res+dp[move][i][j])%mod;   // 如果超出边界，则累加方法数
                       else  dp[move+1][x][y]=(dp[move+1][x][y]+dp[move][i][j])%mod;      // 没有超过边界，则把上一步位置的方法数累加
                }
            }
     }
     return res;
    }
};

记忆化搜索：

class Solution {
public:
    // 记忆化搜索到底是什么出发点？是以哪个为基准？
    // 感觉是个往回收的感觉，最终方法数和统计在起始点上！！！！
    vector<vector<int>> dir={{1,0},{0,1},{-1,0},{0,-1}};
    int dp[55][55][55];
    int mod=1e9+7;
    int N,M;
    int dfs(int x,int y,int leftstep)   //  求(x,y)位置剩余leftstep步数，状态方法数
    {
        if (x<0 || x>=M || y<0 || y>=N) return 1;  // 表明是一种方法
        if (leftstep==0) return 0;
        if (dp[leftstep][x][y]!=-1) return dp[leftstep][x][y];  // 说明这种状态已经遍历过了
        int ans=0;
        for(auto d:dir)
        {
            int xx=x+d[0];
            int yy=y+d[1];
            // dp[leftstep][x][y]=(dp[leftstep][x][y]+dfs(xx,yy,leftstep-1))%mod;  //  不能一步步加，这样递归到后面的时候，这个状态为被认为已经访问过，就有问题，其实还没有访问过
            ans=(ans+dfs(xx,yy,leftstep-1))%mod;  // 需要先用一个变量存起来，然后统一赋值
        }
        //  或者dp[leftstep][x][y]=(dfs()+dfs()+dfs()+dfs())%mod;
        return dp[leftstep][x][y]=ans;
    }
    int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
    memset(dp,-1,sizeof(dp));   // 不能赋值为0，因为上面不能达到为0，所以没访问过的状态应该用-1
    N=n;
    M=m;
    return dfs(startRow,startColumn,maxMove);
    }
};