二叉树的重建
几乎所有的人都知道二叉树可以根据前序遍历+中序遍历或者后序遍历+中序遍历的方式重新建立原来的二叉树,并且结果是唯一的。下面就来看一下相关的方法。
前序+中序重建二叉树
给定一棵二叉树的前序和中序遍历序列,重新建立这棵二叉树。
注意:在前序中确定了根节点以后,要去中序里面查找这个根节点,这时的查找没必要从数组的0下面开始,从这个树的中序的第一个点开始。然后查找的个数为停止的下表减去中序开始的下表。
这里重建二叉树用的是递归的方法,要注意递归的出口。不然会死循环。
所以代码实现:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
int preStart = 0;
int preLast = preorder.size() - 1;
int inStart = 0;
int inLast = inorder.size() - 1;
return SubTreeBuild(preorder, preStart, preLast, inorder, inStart, inLast);
}
TreeNode* SubTreeBuild(vector<int>& preorder, int preStart, int preLast, vector<int>& inorder, int inStart, int inLast)
{
if(preStart > preLast || inStart > inLast)
return NULL;
TreeNode *root = new TreeNode(preorder[preStart]);
//search the root in the inorder
int i = inStart;
while(inorder[i] != preorder[preStart])
{
++i;
}
root->left = SubTreeBuild(preorder, preStart + 1, preStart + i - inStart, inorder, inStart, i - 1);
root->right = SubTreeBuild(preorder, preStart + 1 + i - inStart, preLast, inorder, i + 1, inLast);
return root;
}//SubTreeBuild
后序+中序重建二叉树
其实递归的方式并不是难点,重要的是定边界值。
TreeNode* SubTreeBuild(vector<int>& inorder, int ileft, int iright, vector<int>& postorder, int pleft, int pright)
{
if(ileft > iright || pleft > pright)
return NULL;
TreeNode *root = new TreeNode(postorder[pright]);
//search the root node in the inorder
int i = ileft;
while(inorder[i] != postorder[pright])
{
++i;
}
root->left = SubTreeBuild(inorder, ileft, i - 1, postorder, pleft, pleft + i - ileft - 1);
root->right = SubTreeBuild(inorder, i + 1, iright, postorder, pleft + i - ileft, pright - 1);
return root;
}
二叉树的序列化和反序列化
二叉树的建立
将二叉树中的没个结点的空指针引出一个虚节点,其值为一个特定值,比如说#字符,我们成这种处理后的二叉树为原来二叉树的扩展二叉树。扩展二叉树和二叉树是一一对应关系。
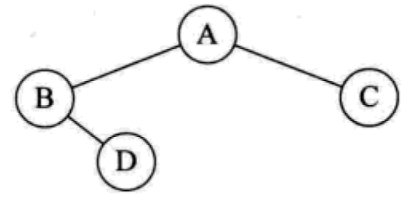
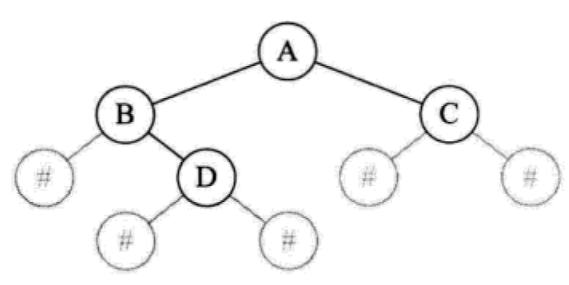
所以前序的序列化序列为:AB#D##C##
序列化二叉树或者是反序列化二叉树就是二叉树和扩展二叉树遍历序列之间的转换。
序列化的意思是将内存中的一些特定的结构,变成有格式信息的字符串。
所谓的二叉树的序列化,是将一个结构化的东西变成扁平化的字符串。这样可以方便传输和进行压缩等。使用BFS或者DFS的方法在面试中都是正确的,但如果能够比较出BFS的方法可以更有效的节省空间的话,可以得到额外的加分。
看下面的这个树:

分别选用DFS的前序序列化和BFS的层次遍历得到的结果是:
DFS:3 9 # # 20 # 15 # # 7
BFS:3 9 20 # # 15 7
LintCode:
http://www.lintcode.com/zh-cn/problem/binary-tree-serialization/#