前面介绍的几种查找的算法都是基于数据有序的基础上进行的。但是在实际的应用中,很多数据集可能有惊人的数据量,面对这些海量的数据,要保证记录全部按照当中的某个关键字有序,其时间代价是非常昂贵的,所以这种数据通常都是按先后顺序存储的。
那么如何能够快速的查找到需要的数据呢?办法就是--索引。
索引就是把一个关键字与它对应的记录相关联的过程。一个索引有若干个索引项构成,每个索引项至少应包括关键字和对应的记录在存储器中的位置等信息。
在索引表中的每个索引项对应多条记录,则称为稀疏索引,若每个索引项唯一对应一条记录,则称为稠密索引。
索引按照结构可以分为线性索引、树形索引和多级索引。所谓的线性索引就是将索引项集合组织为线性结构,也称为索引表。
稠密索引
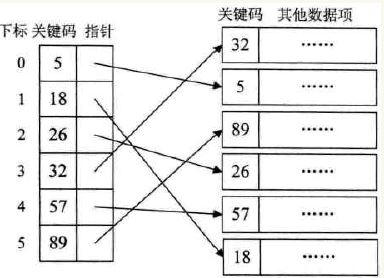
稠密索引是指在线性索引表中,将数据集中的每个记录对应一个索引项。并且索引项一定是按照关键码有序的排列。
索引项有序也就意味着,在查找关键字时,可以用到折半、插值、斐波那契等有序的查找算法。
稠密索引的改进的地方在于:它简化了庞大的原数据集,使原本不能装入内存的庞大的数据集,能一次性的装入内存,并且能够在内存中实现关键字码的排序,并且每一个索引项能够指向磁盘中它代表的原数据记录。
能利用高级的查找算法,这显然是稠密索引的优点,但是如果数据集非常的大,那么索引表也是非常的大,对于内存有限的计算机来说,不得不把索引表也放到磁盘中,这样就大大的降低了效率。
分块索引
稠密索引因为索引项与数据集的记录个数相同,所以空间代价很大。为了减少索引项的个数,对数据集进行分块,使其分块有序,然后在对每一块建立一个索引项,从而减少索引项的个数。
分块有序,就是把数据集的记录分成了若干块,这些块需要满足的条件是:
块内无序,块间有序。

上图中定义的索引项的结构分为三个数据项:
(1)最大关键码,它存储了每一块中的最大关键字,这样的好处是可以使得在它之后的下一块中的最小关键字也能比这一块最大的关键字要大。当然这个索引关键字码可以是任何能够唯一标识一个块的任何数据。
(2)存储了块中记录的个数,以便于循环时使用。
(3)用于指向块首数据元素的指针,便于开始对这一块中记录遍历
分块索引如果在索引表和每个块内的记录都采用顺序表查找,那么时间复杂度分析就如下:
分块索引表的平均查找长度分析
设有n个记录,被分成了m块,每块有t条记录。显然n=mxt。在索引表和块中的平均查找长度分别是Lb和Lw。

上面的分析中,在块间使用的也是顺序查找,因为块间是有序的,所以可以使用折半查找等快速的算法来提高效率。

#define ILMSize 60;
#define MaxSize 3600;
//建立索引项结构
struct IndexItem
{
int index;
int start;
int length;
};
//建立索引表
typedef struct IndexItem indexList[ILMSize]; //ILMSize为事先定义好的整型常量,大于等于索引项数目m
//建立原始数据的主表
int mainList[MaxSize]; //MaxSize为事先定义好的整型常量,大于等于主表中的记录的个数n
/*
* 输入:主表A,索引表B,索引表中索引项数目m,要搜索的元素elem
* 输出:找到的元素的下标
*/
int blockSearch(mainList A, indexList B, int m, int elem)
{
for(int i = 0; i < m; i++)
{
if(B[i].index >= elem)
{
break;
}
}//for
if(i == m)
{
return -1; //查找失败
}
int endNum = B[i].start + B[i].length;
for(int j = B[i].start; j < num; j++)
{
if(A[j] == elem)
{
break;
}
}//for
if(j < num)
{
return j;
}
if(j == num)
{
return -1;
}
}
若 IndexKeyType 被定义为字符串类型,则算法中相应的条件改为
strcmp (K1, B[i].index) == 0;
同理,若KeyType 被定义为字符串类型
则算法中相应的条件也应该改为
strcmp (K2, A[j].key) == 0
若每个子表在主表A中采用的是链接存储,则只要把上面算法中的while循环
和其后的if语句进行如下修改即可:
while (j != -1)//用-1作为空指针标记
{
if (K2 == A[j].key)
break;
else
j = A[j].next;
}
return j;
在索引表中折半查找的伪代码
//在索引表中折半查找伪代码 while low <= high mid = (low + high)/2 if A[mid-1]<elem<A[mid] i = mid break else if A[mid-1]>elem high = mid - 1 else if elem > A[mid] low = mid + 1 if low > high i = low
在索引表中折半查找的代码实现
//在索引表中折半查找代码实现
while(low <= high)
{
mid = (low + high) / 2;
if(B[mid -1].index < elem && B[mid].index > elem)
{
i = mid;
break;
}
else if(B[mid - 1].index > elem)
{
high = mid - 1;
}
else
{
low = mid + 1;
}
}//while
if(low > high)
{
i = low;
}
分块索引表的建立
这样就能很好的实现,大的数据块存储在磁盘上,索引表存储于内存中了。这种模型是不需要对原始数据集进行排序操作的,因为块与块之间是可以不连续的存放的。在原始数据产生前确定分多少块,以及每个块的存储位置(块间位置不连续,块内位置连续),这时每个块内的存储数据的范围也要确定,当新的数据到来的时候,就能确定要把这个数据放到哪个块中。
举个例子:
我想设计一个分块索引来查找数据,大体估算有3600个数据,所以根据能使算法效率最高的分块数目等于每一块的记录数目。设置60个块,每个块有60个记录。60个块就对应磁盘上的60个文件夹目录用来存储数据,这60个块的块间位置不连续。同时假设这3600个记录的关键字大小范围是1-3000,那么第一块就存储1-50的记录。来一个新纪录,如果关键字在1-50之间,就直接把它追加到第一块中。同时如果这个记录的关键字值大于索引表中的最大关键码,就对索引表中的最大关键字码更新。
参考文章链接
http://blog.csdn.net/wtfmonking/article/details/17337703
http://blog.csdn.net/xiaoping8411/article/details/7706381
http://blog.csdn.net/xiaoping8411/article/details/7706376
http://blog.csdn.net/wangyunyun00/article/details/23464359
http://blog.csdn.net/fovwin/article/details/9077017