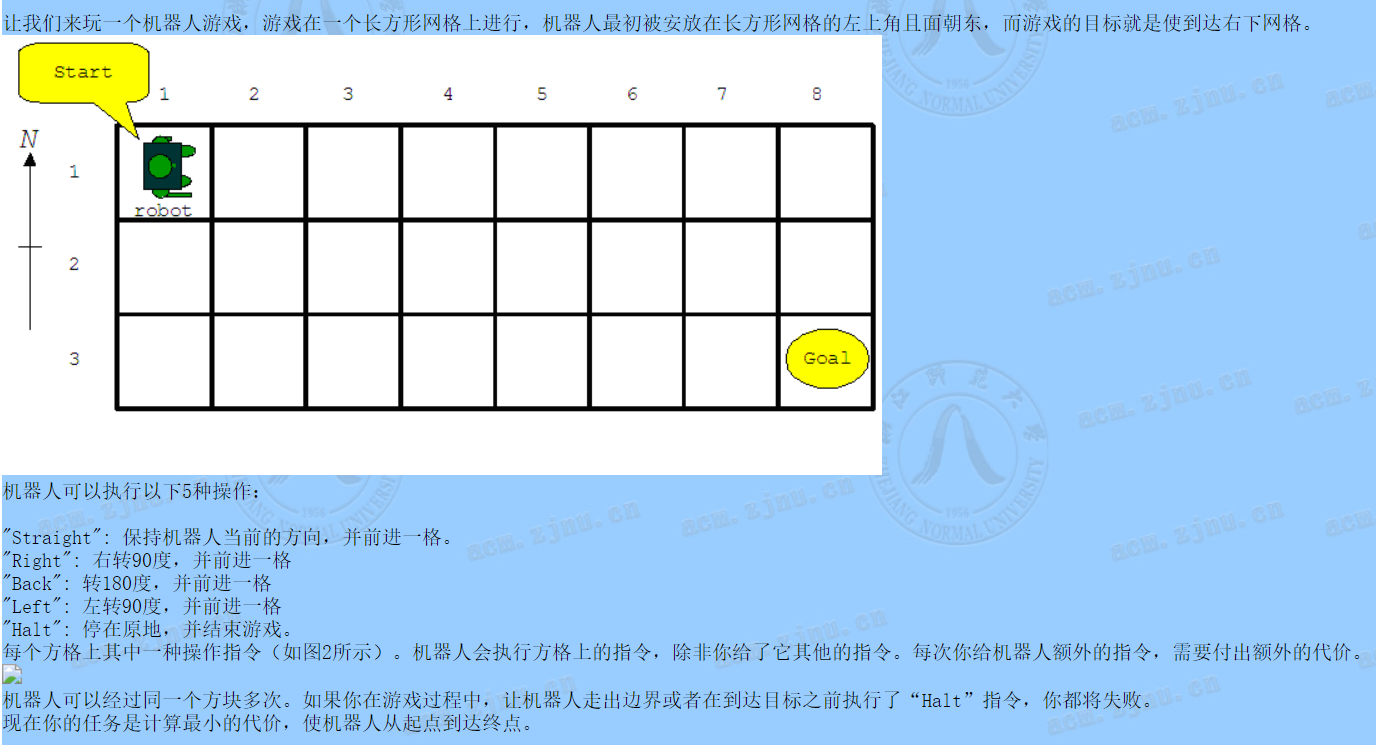
题面
思路
直接搜索,按照图中给定的指令操作不会产生任何花费
特殊的,可以给定特殊的指令让机器人无视此时图中的指令,因此可以将所有情况全部加入搜索中,寻找最短路即可
另外,本题中还有方向的限制,所以每个点都具有上下左右四种状态,故定义(dis[i][j][k])表示到了((i,j))点并且朝向为(k)的最短路
进行SPFA搜索,最后将(sum_{i=0}^3 dis[n][m][i])取小作为答案即可
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define all(a) (a).begin(),(a).end()
#define SUM(a) accumulate(all(a),0LL)
#define MIN(a) (*min_element(all(a)))
#define MAX(a) (*max_element(all(a)))
#define mst(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define eb emplace_back
#define fi first
#define se second
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const ll mod=998244353;
void debug(){cerr<<'
';}template<typename T,typename... Args>void debug(T x,Args... args){cerr<<"[ "<<x<< " ] , ";debug(args...);}
mt19937 mt19937random(std::chrono::system_clock::now().time_since_epoch().count());
ll getRandom(ll l,ll r){return uniform_int_distribution<ll>(l,r)(mt19937random);}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}
struct node
{
int d,x,y;
node(){}
node(int d,int x,int y):d(d),x(x),y(y){}
};
int n,m,mp[35][35];
int dis[4][35][35];
bool vis[4][35][35];
int cost[5];
const int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
inline bool prim(int x,int y)
{
return x>0&&y>0&&x<=n&&y<=m;
}
void solve()
{
cin>>m>>n;
rep(i,1,n)
rep(j,1,m)
cin>>mp[i][j];
rep(i,0,3)
cin>>cost[i];
mst(dis,INF);
queue<node> q;
q.push(node(1,1,1));
dis[1][1][1]=0;
while(!q.empty())
{
node nd=q.front();
q.pop();
int &x=nd.x,&y=nd.y;
vis[nd.d][x][y]=false;
if(mp[x][y]==0)
{
int d=nd.d;
int px=x+dx[d],py=y+dy[d];
if(prim(px,py))
{
if(dis[d][px][py]>dis[nd.d][x][y])
{
dis[d][px][py]=dis[nd.d][x][y];
if(!vis[d][px][py])
{
vis[d][px][py]=true;
q.push(node(d,px,py));
}
}
}
}
else if(mp[x][y]==1)
{
int d=(nd.d+1)%4;
int px=x+dx[d],py=y+dy[d];
if(prim(px,py))
{
if(dis[d][px][py]>dis[nd.d][x][y])
{
dis[d][px][py]=dis[nd.d][x][y];
if(!vis[d][px][py])
{
vis[d][px][py]=true;
q.push(node(d,px,py));
}
}
}
}
else if(mp[x][y]==2)
{
int d=(nd.d+2)%4;
int px=x+dx[d],py=y+dy[d];
if(prim(px,py))
{
if(dis[d][px][py]>dis[nd.d][x][y])
{
dis[d][px][py]=dis[nd.d][x][y];
if(!vis[d][px][py])
{
vis[d][px][py]=true;
q.push(node(d,px,py));
}
}
}
}
else if(mp[x][y]==3)
{
int d=(nd.d+3)%4;
int px=x+dx[d],py=y+dy[d];
if(prim(px,py))
{
if(dis[d][px][py]>dis[nd.d][x][y])
{
dis[d][px][py]=dis[nd.d][x][y];
if(!vis[d][px][py])
{
vis[d][px][py]=true;
q.push(node(d,px,py));
}
}
}
}
rep(i,0,3)
{
int d=(nd.d+i)%4;
int px=x+dx[d],py=y+dy[d];
if(prim(px,py))
{
//cout<<px<<' '<<py<<' '<<dis[d][px][py]<<' '<<dis[d<<'
';
if(dis[d][px][py]>dis[nd.d][x][y]+cost[i])
{
dis[d][px][py]=dis[nd.d][x][y]+cost[i];
if(!vis[d][px][py])
{
vis[d][px][py]=true;
q.push(node(d,px,py));
}
}
}
}
}
cout<<min({dis[0][n][m],dis[1][n][m],dis[2][n][m],dis[3][n][m]})<<'
';
// rep(i,1,n)
// rep(j,1,m)
// cout<<min({dis[0][i][j],dis[1][i][j],dis[2][i][j],dis[3][i][j]})<<'
';
}
int main()
{
closeSync;
//multiCase
{
solve();
}
return 0;
}