Codeforces 1492D

Codeforces Round #704 (Div. 2) D. Genius's Gambit

题意

要求构造出两个不包含前导0的二进制数字(x,y)，满足：

• (x,y)都具有(a)个(0)和(b)个(1)
• (x-y)具有(k)个(1)

限制

(age 0)

(bge 1)

(0le kle a+ble 2cdot 10^5)

思路

显然的，由于要求(x,y)不包含前导(0)，故两数字最高位必定为(1)

---

特殊讨论(k=0)时，根据上述约束，直接输出两个字符串即可

注意先输出(b)个(1)再输出(a)个(0)

---

否则，观察样例，自己多写几个例子，可以发现这个规律

中间位对应都相同时，计算减法可以直接当作(X-X=0)

那么假如这一段的长度为(t)，减数最高位为(1)，被减数最低位为(1)，其余(t-1)个位置均为(0)

那做减法得到的结果即(2^{t-1}-1)，其二进制则包含(t-1)个(1)

---

那么只要(k eq 0)，就需要保证至少要有(2)个(1)与(1)个(0)，且(kle a+b-2)

答案总体可以分成以下三个部分（其中后两个部分位置可以随意调换）

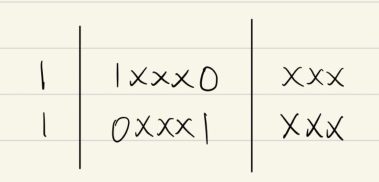
程序

#include<bits/stdc++.h>
using namespace std;

void solve()
{
    int a,b,k;
    cin>>a>>b>>k;
    
    if(k==0)
    {
        cout<<"Yes
";
        for(int i=1;i<=b;i++) cout<<1;
        for(int i=1;i<=a;i++) cout<<0;
        cout<<'
';
        for(int i=1;i<=b;i++) cout<<1;
        for(int i=1;i<=a;i++) cout<<0;
        cout<<'
';
        return;
    }
    
    if(a<1||b<2||k>a+b-2)
    {
        cout<<"No
";
        return;
    }
    
    string x="1",y="1";
    b--;
    
    x+='1',y+='0';
    a--,b--;
    
    for(int i=1;i<k;i++)
    {
        if(a>0)
        {
            a--;
            x+='0',y+='0';
        }
        else if(b>0)
        {
            b--;
            x+='1',y+='1';
        }
    }
    
    x+='0',y+='1';
    
    while(a--)
        x+='0',y+='0';
    while(b--)
        x+='1',y+='1';
    
    cout<<"Yes
"<<x<<'
'<<y<<'
';
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    solve();
    return 0;
}

https://blog.csdn.net/qq_36394234/article/details/113999097