题意
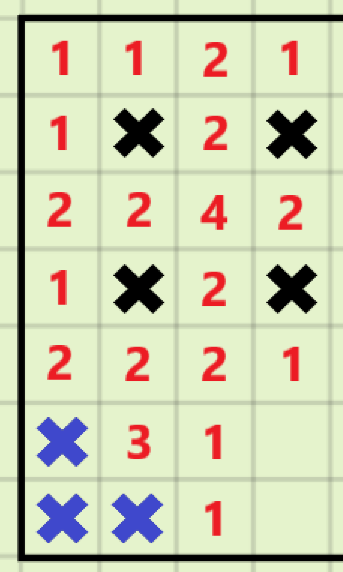
定义《扫雷》游戏的地图中每个空白格子的值为其周围八个格子内地雷的数量(即游戏内临近地雷数量的提示)
则一张地图的值(S)为所有空白格子的值总和
现给定(S),要求构造出一张长度与宽度均不超过(25)的地图,使其值等于(S)
限制
(1leq Tleq 1001)
(0leq Sleq 1000)
思路
这题过的人数应该是最多的,所以肯定是存在比我的想法更优更方便的解的
但是题解写的不是很清楚,所以还是写下了这篇博客(画图好累……)
发现(T_{max}=|S|),范围内每个值肯定都会问一遍,考虑预处理所有方案(在线输出好像也没有问题的样子)
首先发现,如果一个地雷周围没有其他地雷,也没有障碍物(表示它不在图的边界上)
那么这个地雷对于答案的贡献就是(8)
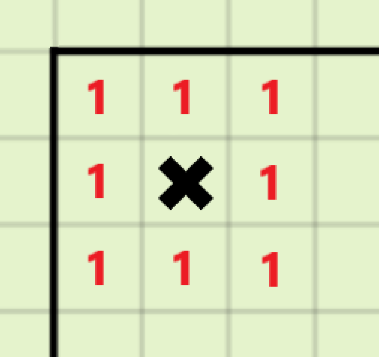
考虑所有地雷都互不相邻的情况(一个地雷周围一圈不存在其他地雷)
由于图最大尺寸为(25 imes 25)
地雷分布情况为((2,2),(2,4),dots,(2,24),(4,2),(4,4),dots,(24,24))
这样总共能放置(12 imes 12=144)个对答案贡献为(8)的地雷
由于(144 imes 8>1000),这样的分布绰绰有余
所以得到一个结论:只要(S)为(8)的倍数,那么它一定有解
首先考虑(Slt 8)的所有情况
当(S=0)时,直接输出一个(1 imes 1)的空图即可
当(S=1)时

当(S=2)时

当(S=3)时

当(S=4)时

当(S=5)时

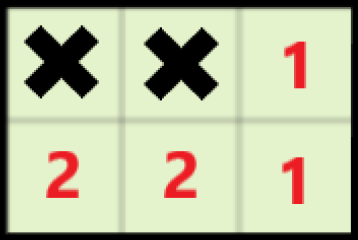
当(S=6)时
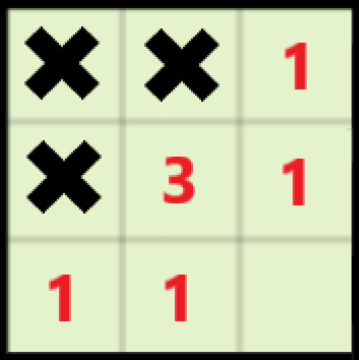
当(S=7)时
既然已经能够确定一个数的倍数一定有解了,那我们可以尝试找找看能否依托(8)来找出其他情况
也就是把(Sgeq 8)的所有情况看成以下的形式之一表示
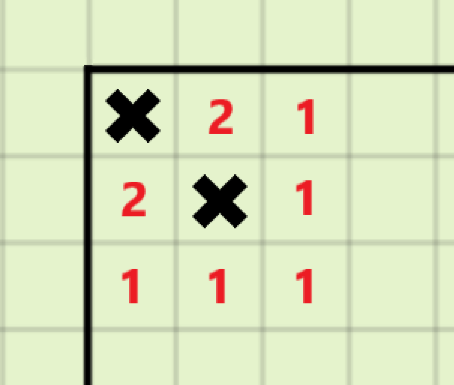
对于(S=8k+1)的情况:
在((1,1))的位置多放置一个地雷,可以使得原本位于((2,2))的地雷对答案的贡献由(8)变成(9),且不影响其他地雷的贡献
对于(S=8k+2)的情况:
在((1,1))与((1,2))的位置多放置两个地雷,可以使得原本位于((2,2))的地雷对答案的贡献由(8)变成(10),且不影响其他地雷的贡献
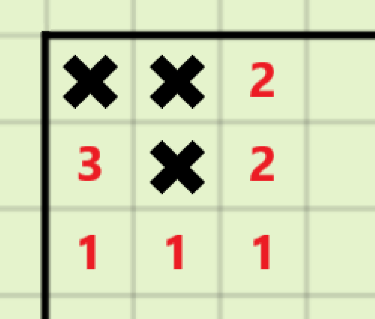
对于(S=8k+3)的情况:
在((1,2))的位置多放置一个地雷,可以使得原本位于((2,2))的地雷对答案的贡献由(8)变成(11),且不影响其他地雷的贡献
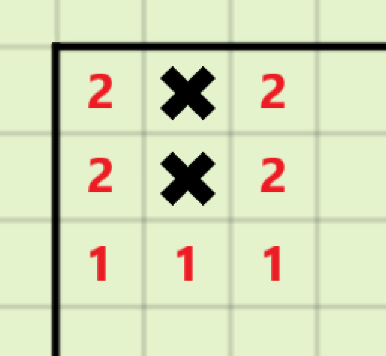
对于(S=8k+4)的情况:
在((1,2))与((2,1))的位置多放置两个地雷,可以使得原本位于((2,2))的地雷对答案的贡献由(8)变成(12),且不影响其他地雷的贡献

对于(S=8k+5)的情况:
仅先看放置贡献为(8)的地雷,假设最后一个放置的地雷位于第(i)行
为了不影响它对答案的贡献,那么第(i+1)行不能放东西
由上面(S=5)的情况可得,我们可以将其上下倒置放在第(i+2)行,从而防止其对其他地雷贡献造成影响
(边界限制可行性证明在下面)
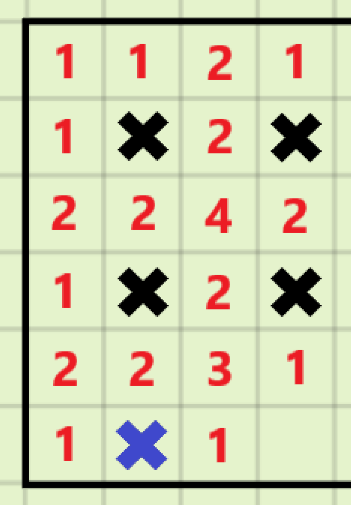
对于(S=8k+6)的情况:
参考(S=6),同样的,为了不产生冲突,只能放置在第(i+2)行
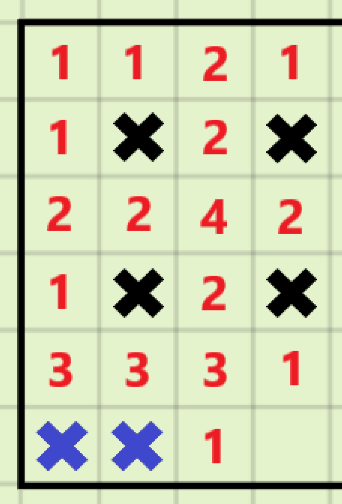
对于(S=8k+7)的情况:
由于(S=7)的情况里地雷需要占两行
所以要将(S=7)的情况倒置放在(S=8k)的第(i+2)行与第(i+3)行
(边界限制可行性证明在下面)
直接证明(S=8k+7)时需要用到(i+3)行的可行性情况吧
由于(S)最大为(1000),如果全部使用贡献为(8)的地雷方案填充地图,最多只需要(125)个地雷
每行最多能放置(12)个这种方案的地雷,那么最多只需要用到第(11)行过
对于原图,由于地雷在行之间也需要空一行,故(i)的最大值为(22)
(22+3=25),恰好满足题目要求,故方案可行
综上,本题所有(S)情况均有解,预处理后直接输出即可
注意,(S=8k)的情况最后也需要输出(i+1)行(最后一行空着,以保证有空格子让地雷做出贡献,即让最后一行的地雷非边界)
示例
如果没大看懂上面的例子,这里放几张截图领会一下大致意思即可
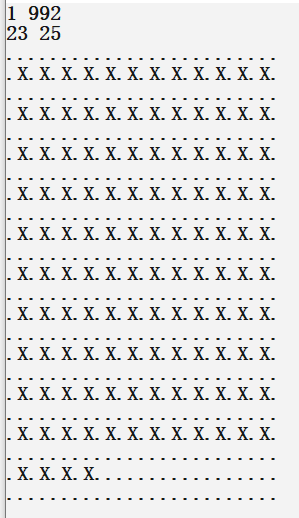
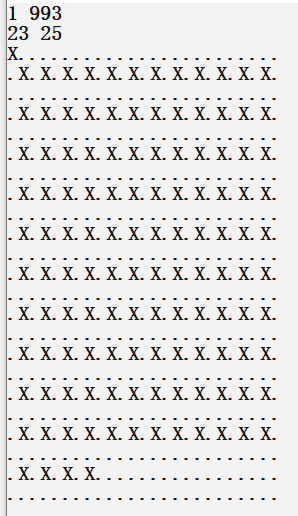






代码
(0ms~31ms/1000ms)
#include<bits/stdc++.h>
using namespace std;
int mp[1010][28][28];
int maxCol[1010];
void init()
{
for(int i=8;i<=1000;i++)
{
int les=i/8,j,k;
for(j=2;j<=24;j+=2)
{
for(k=2;k<=24;k+=2)
{
mp[i][j][k]=1;
if(--les==0)
break;
}
if(les==0)
break;
}
switch(i%8)
{
case 0:
maxCol[i]=j+1;
break;
case 1:
mp[i][1][1]=1;
maxCol[i]=j+1;
break;
case 2:
mp[i][1][1]=mp[i][1][2]=1;
maxCol[i]=j+1;
break;
case 3:
mp[i][1][2]=1;
maxCol[i]=j+1;
break;
case 4:
mp[i][1][2]=mp[i][2][1]=1;
maxCol[i]=j+1;
break;
case 5:
mp[i][j+2][2]=1;
maxCol[i]=j+2;
break;
case 6:
mp[i][j+2][1]=mp[i][j+2][2]=1;
maxCol[i]=j+2;
break;
case 7:
mp[i][j+3][1]=mp[i][j+3][2]=mp[i][j+2][1]=1;
maxCol[i]=j+3;
break;
}
}
}
int main()
{
init();
int T,S;
scanf("%d",&T);
while(T--)
{
scanf("%d",&S);
if(S>=8)
{
printf("%d 25
",maxCol[S]);
for(int i=1;i<=maxCol[S];i++)
{
for(int j=1;j<=25;j++)
{
if(mp[S][i][j])
putchar('X');
else
putchar('.');
}
putchar('
');
}
}
else if(S==0)
{
puts("1 1");
puts(".");
}
else if(S==1)
{
puts("1 2");
puts("X.");
}
else if(S==2)
{
puts("1 3");
puts("X.X");
}
else if(S==3)
{
puts("2 2");
puts("X.");
puts("..");
}
else if(S==4)
{
puts("2 2");
puts("X.");
puts("X.");
}
else if(S==5)
{
puts("2 3");
puts(".X.");
puts("...");
}
else if(S==6)
{
puts("2 3");
puts("XX.");
puts("...");
}
else if(S==7)
{
puts("3 3");
puts("XX.");
puts("X..");
puts("...");
}
}
return 0;
}