题意
给定(n,m),在坐标系((0,0)) 位置有一个能量采集器
可行范围为(n imes m)内的所有整数点(不包括坐标轴上)
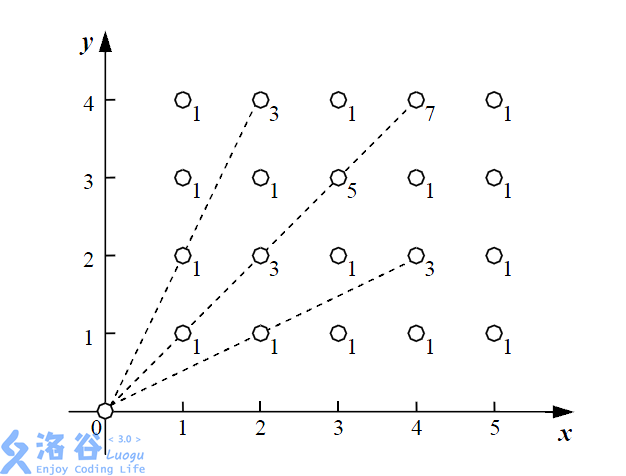
开采每个整数点会造成(1)能量损失
对于每个点((x,y)),如果((0,0))与其连线上存在着(cnt)个其它整数点,那么它的能量损失将会增加(2 imes cnt)
即对于每个点,能量损失为(2 imes cnt_{(x,y)}+1)
求(n imes m)范围内所有点的能量损失之和,即求
[sum_{i=1}^nsum_{j=1}^m2 imes cnt_{(x,y)}+1
]
限制
(Case=1, 1leq n,mleq 10^5)
思路
根据题意(或据图可得)
每个点((x,y))与((0,0))点连线上的其余整数点个数即为(gcd(x,y)-1)
所以所求的答案即可转化为
[egin{align}
&sum_{i=1}^nsum_{j=1}^m2 imes (gcd(i,j)-1)+1\
=&sum_{i=1}^nsum_{j=1}^m2 imes gcd(i,j)-1\
=&2 imes sum_{i=1}^nsum_{j=1}^m(gcd(i,j))-n imes m\
=&2 imes sum_{d=1}^{min(n,m)}d imessum_{i=1}^nsum_{j=1}^m[gcd(i,j)=d] -n imes m\
=&2 imes sum_{d=1}^{min(n,m)}d imessum_{i=1}^{frac n d}sum_{j=1}^{frac m d}[gcd(i,j)=1] -n imes m\
=&2 imes sum_{d=1}^{min(n,m)}d imessum_{i=1}^{frac{min(n,m)}{d}}mu(i)lfloorfrac{lfloorfrac n d
floor}{i}
floorlfloorfrac{lfloorfrac m d
floor}{i}
floor -n imes m\
end{align}
]
直接套板子即可
代码
Case Max (15ms/1000ms)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100000;
ll mu[N+50],prim[N+50];
bool vis[N+50];
void init(int n)
{
memset(vis,false,sizeof vis);
mu[1]=1;
int p=0;
for(int i=2;i<=n;i++)
{
if(!vis[i])
{
prim[p++]=i;
mu[i]=-1;
}
for(int j=0;j<p;j++)
{
int k=i*prim[j];
if(k>n)
break;
vis[k]=true;
if(i%prim[j]==0)
{
mu[k]=0;
break;
}
else
mu[k]=-mu[i];
}
}
}
int main()
{
init(N);
int n,m;
scanf("%d%d",&n,&m);
ll ansd,ans=0;
int mn=min(n,m);
for(int d=1;d<=mn;d++)
{
int mnd=mn/d,a=n/d,b=m/d;
ansd=0;
for(int i=1;i<=mnd;i++)
ansd+=mu[i]*(a/i)*(b/i);
ans+=ansd*d;
}
printf("%lld
",ans*2-1LL*n*m);
return 0;
}