【数据结构】倍增算法

后缀数组的倍增算法

后缀数组

算法介绍

　　先根据字符串中字符的出现情况，给每一种字符一个对应的排名（从1开始），作为第一次排序的结果

　　其后每一次，每个位置以当前排名作为主关键词，从1开始倍增步数，将对应的位置排名作为第二关键词

　　于是根据主关键词与副关键词继续给定排名，作为当次排序的结果

　　如果加上倍增的步数后超出了字符串长度Len，则副关键词排名为 0

　　如此循环，直到第一个位置加上倍增步数后超出字符串长度为止，算作算法结束，此时得到的排序结果即为sa数组

　　总共排序次数为 logn

　　若排序使用快排O(nlogn)，则总时间复杂度为O(nlog²n)

　　若使用基数排序，则可将排序复杂度降至O(n)，总复杂度降为O(nlogn)

　　经典基数排序图示：

　　

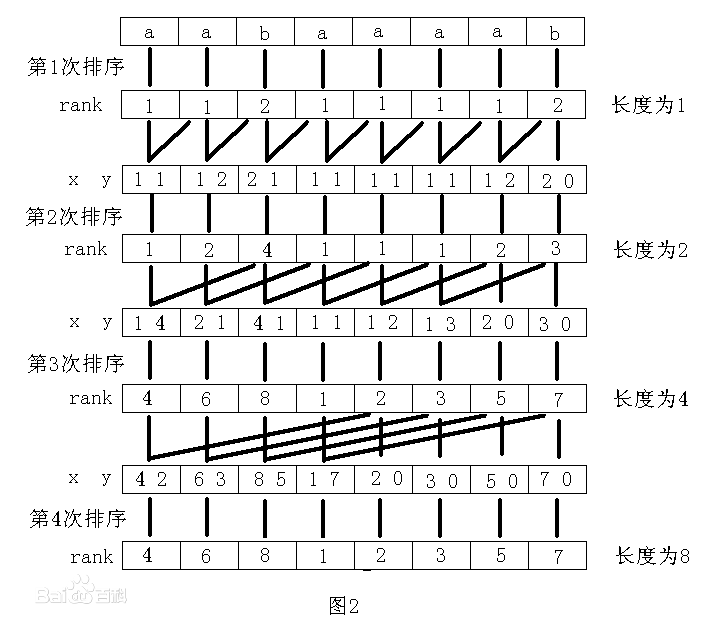
模板

完全看懂太难了，学会用法后复制粘贴吧

const int N=100050;

int xx[N],yy[N],cnt[N]; //缓存数组
int sa[N],rk[N],height[N]; //结果
char str[N]; //字符串

倍增求sa

void getSA_DA(int n,int M) //n=length+1，M表示待处理字符串最大可能拥有的字符种类
{
    int i,j,p,*x=xx,*y=yy;
    for(i=0;i<M;i++)
        cnt[i]=0;
    for(i=0;i<n;i++)
        cnt[x[i]=str[i]]++;
    for(i=1;i<M;i++)
        cnt[i]+=cnt[i-1];
    for(i=n-1;i>=0;i--)
        sa[--cnt[x[i]]]=i; //根据原字符串求出每个字符的初始排名
    for(j=1,p=1;p<n;j<<=1,M=p) //倍增步数j
    {
       for(p=0,i=n-j;i<n;i++)
           y[p++]=i; //取第二关键词
       for(i=0;i<n;i++)
           if(sa[i]>=j)
               y[p++]=sa[i]-j;
       for(i=0;i<M;i++)
           cnt[i]=0;
       for(i=0;i<n;i++)
           cnt[x[y[i]]]++;
       for(i=1;i<M;i++)
           cnt[i]+=cnt[i-1];
       for(i=n-1;i>=0;i--)
           sa[--cnt[x[y[i]]]]=y[i];
       swap(x,y); //交换两数组指针（交替使用）
       p=1;x[sa[0]]=0;
       for(i=1;i<n;i++)
           if(y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+j]==y[sa[i]+j])
               x[sa[i]]=p-1;
           else
               x[sa[i]]=p++;
    }
}

　　使用指针来指向缓存数组，便于进行指针交替

　　需要注意的是，这里的 n == len+1 ，字符串最后一个位置置零处理（读入自动添加''结束符时可以略过）

　　M 表示字符串拥有的字符最大种类数

　　此时求出的sa数组的内容编号从0开始，内容+1才是所求编号

求rk与height数组

void getHeight(int n) //n=length
{
    int i,j,k=0;
    for(i=1;i<=n;i++) //导出rk数组
        rk[sa[i]]=i;
    for(i=0;i<n;)
    {
        if(k)k--; //根据关系，本次LCP最小值为上一次的LCP-1
        j=sa[rk[i]-1];
        while(str[i+k]==str[j+k]) //在k的基础上继续遍历判断LCP
            k++;
        height[rk[i++]]=k;
    }
    for(i=n;i;i--) //rk后移，sa增加编号
        rk[i]=rk[i-1],sa[i]++;
}

　　这里的 n==len ，先 O(n) 由sa求出rk数组，再根据关系遍历字符串求出height数组

　　由于前面处理范围为 [0,len-1] ，排名编号从0开始，故最后将rk数组整体后移一位

　　又因为sa内容编号从0开始，故sa自增

DA算法完整模板

#include<bits/stdc++.h>
using namespace std;
const int N=100050;

int xx[N],yy[N],cnt[N];
int sa[N],rk[N],height[N];
char str[N];

void getSA_DA(int n,int M)
{
    int i,j,p,*x=xx,*y=yy;
    for(i=0;i<M;i++)
        cnt[i]=0;
    for(i=0;i<n;i++)
        cnt[x[i]=str[i]]++;
    for(i=1;i<M;i++)
        cnt[i]+=cnt[i-1];
    for(i=n-1;i>=0;i--)
        sa[--cnt[x[i]]]=i;
    for(j=1,p=1;p<n;j<<=1,M=p)
    {
        for(p=0,i=n-j;i<n;i++)
            y[p++]=i;
        for(i=0;i<n;i++)
            if(sa[i]>=j)
                y[p++]=sa[i]-j;
        for(i=0;i<M;i++)
            cnt[i]=0;
        for(i=0;i<n;i++)
            cnt[x[y[i]]]++;
        for(i=1;i<M;i++)
            cnt[i]+=cnt[i-1];
        for(i=n-1;i>=0;i--)
            sa[--cnt[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;x[sa[0]]=0;
        for(i=1;i<n;i++)
            if(y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+j]==y[sa[i]+j])
                x[sa[i]]=p-1;
            else
                x[sa[i]]=p++;
    }
}
void getHeight(int n)
{
    int i,j,k=0;
    for(i=1;i<=n;i++)
        rk[sa[i]]=i;
    for(i=0;i<n;)
    {
        if(k)k--;
        j=sa[rk[i]-1];
        while(str[i+k]==str[j+k])
            k++;
        height[rk[i++]]=k;
    }
    for(i=n;i;i--)
        rk[i]=rk[i-1],sa[i]++;
}
int main()
{
    scanf("%s",str);
    int len=strlen(str);
    getSA_DA(len+1,128);
    getHeight(len);
    
    /*
    for(int i=1;i<=len;i++)
        printf("%d ",sa[i]);
    putchar('
');
    for(int i=1;i<=len;i++)
        printf("%d ",rk[i]);
    putchar('
');
    for(int i=1;i<=len;i++)
        printf("%d ",height[i]);
    putchar('
');
    */
    return 0;
}

行数压缩后模板

#include<bits/stdc++.h>
using namespace std;
const int N=100050;
int xx[N],yy[N],cnt[N];
int sa[N],rk[N],height[N];
char str[N];
void getSA_DA(int n,int M){
    int i,j,p,*x=xx,*y=yy;
    for(i=0;i<M;i++)cnt[i]=0;
    for(i=0;i<n;i++)cnt[x[i]=str[i]]++;
    for(i=1;i<M;i++)cnt[i]+=cnt[i-1];
    for(i=n-1;i>=0;i--)sa[--cnt[x[i]]]=i;
    for(j=1,p=1;p<n;j<<=1,M=p){
        for(p=0,i=n-j;i<n;i++)y[p++]=i;
        for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
        for(i=0;i<M;i++)cnt[i]=0;
        for(i=0;i<n;i++)cnt[x[y[i]]]++;
        for(i=1;i<M;i++)cnt[i]+=cnt[i-1];
        for(i=n-1;i>=0;i--)sa[--cnt[x[y[i]]]]=y[i];
        for(swap(x,y),p=1,x[sa[0]]=0,i=1;i<n;i++)
            x[sa[i]]=(y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+j]==y[sa[i]+j])?p-1:p++;
    }
}
void getHeight(int n){
    int i,j,k=0;
    for(i=1;i<=n;i++)rk[sa[i]]=i;
    for(i=0;i<n;height[rk[i++]]=k)
        for(k?k--:0,j=sa[rk[i]-1];str[i+k]==str[j+k];k++);
    for(i=n;i;i--)rk[i]=rk[i-1],sa[i]++;
}
int main(){
    scanf("%s",str);
    int len=strlen(str);
    getSA_DA(len+1,128);
    getHeight(len);
    
    return 0;
}