题面
Time limit per test: 2 seconds
Memory limit per test: 256 megabytes
Description
You are given a regular polygon with 2⋅n vertices (it's convex and has equal sides and equal angles) and all its sides have length 1. Let's name it as 2n-gon.
Your task is to find the square of the minimum size such that you can embed 2n-gon in the square. Embedding 2n-gon in the square means that you need to place 2n-gon in the square in such way that each point which lies inside or on a border of 2n-gon should also lie inside or on a border of the square.
You can rotate 2n-gon and/or the square.
Input
The first line contains a single integer T (1≤T≤200) — the number of test cases.
Next T lines contain descriptions of test cases — one per line. Each line contains single even integer n (2≤n≤200). Don't forget you need to embed 2n-gon, not an n-gon.
Output
Print T real numbers — one per test case. For each test case, print the minimum length of a side of the square 2n-gon can be embedded in. Your answer will be considered correct if its absolute or relative error doesn't exceed 10^−6^.
Example
input
3
2
4
200
output
1.000000000
2.414213562
127.321336469
题意
给定一个边长为 1 的正 2n 边形
求外接正方形的最小面积
解题思路 1
因为本题给定的 n 是偶数
故正方形与正 2n 边形恰好可以有4条边重合
正八边形如下:
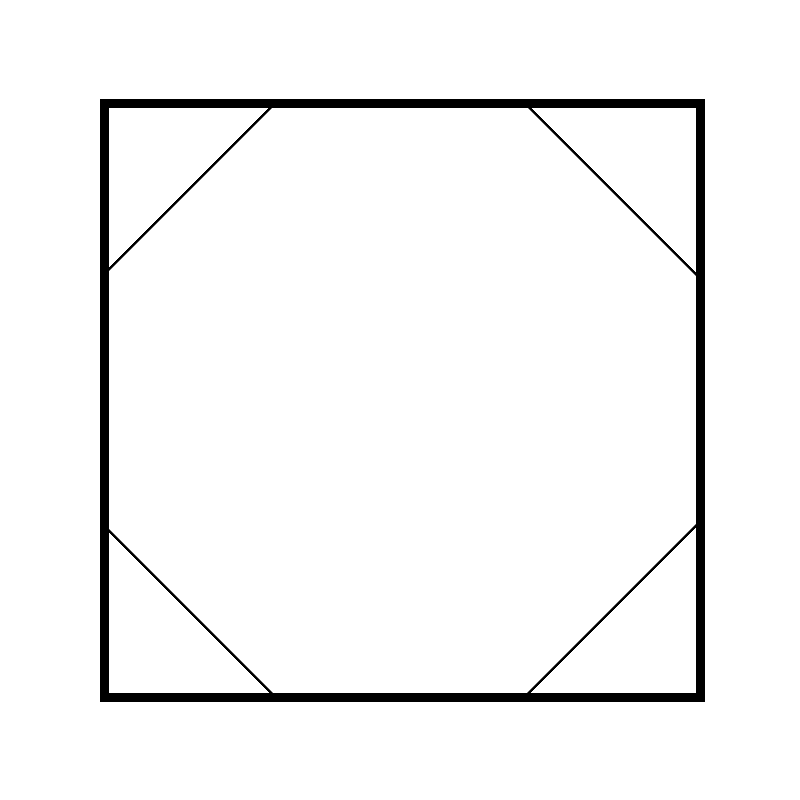
正十二边形如下:
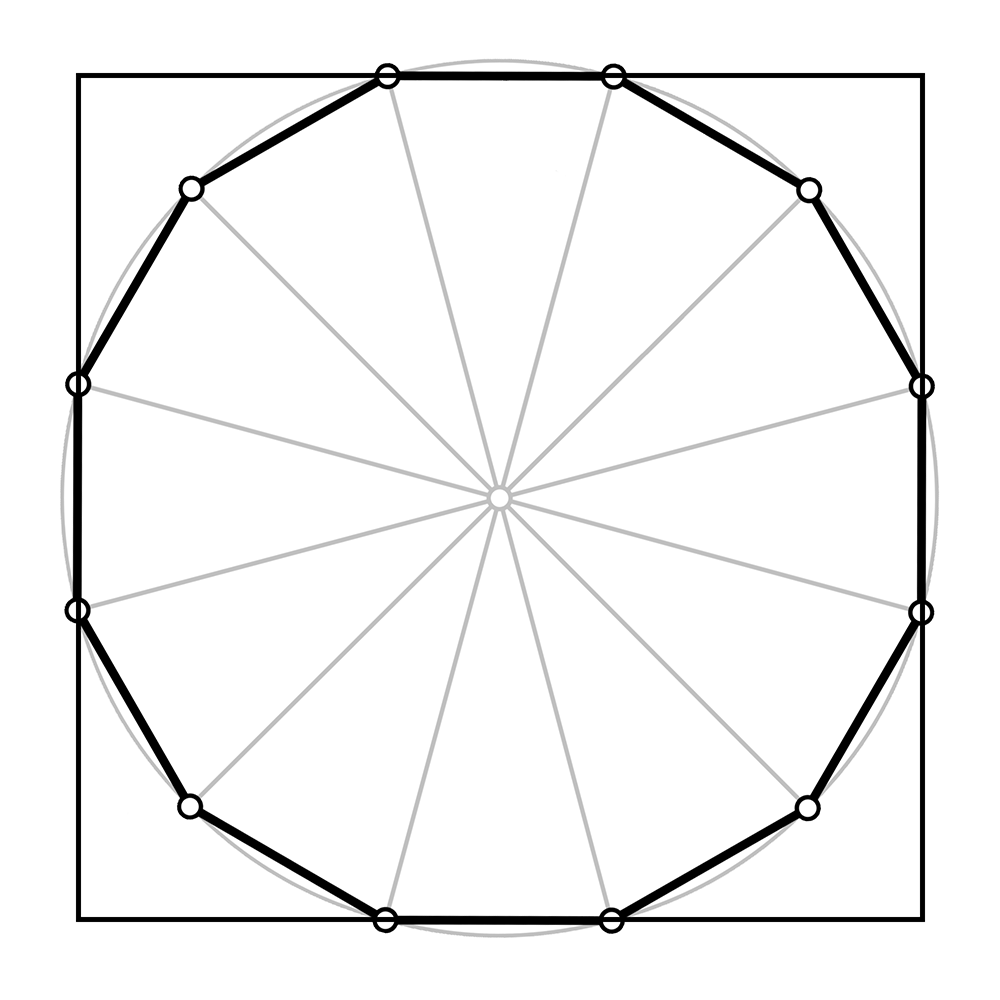
以正十二边形为例,根据对称性,可以先只看右上的部分:
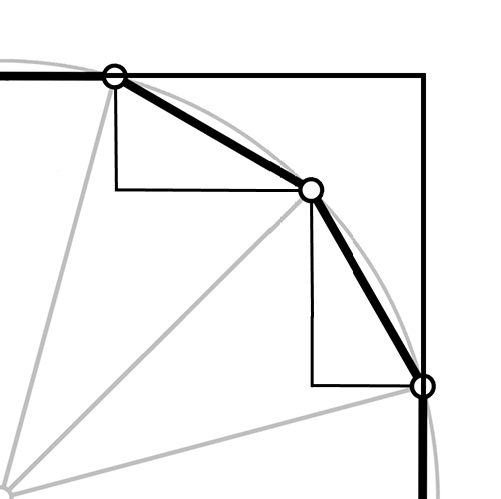
根据正十二边形的每条边再画出水平和竖直的两条边,组成一个直角三角形
可以得到,最上边截得半条边,长度为 1/2
在所有斜边中,因为正多边形角度平分,所以可以得到每条斜边与水平边的夹角是平分90°角的
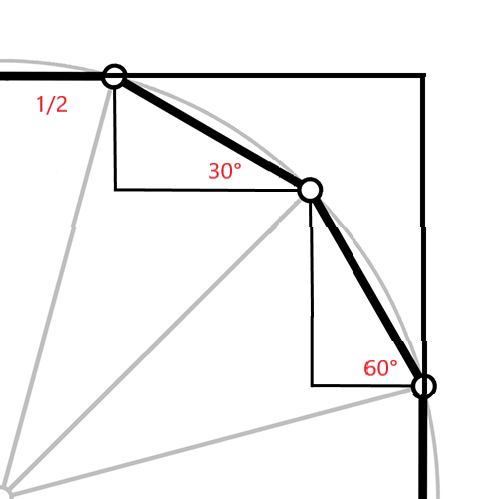
所以这张图中的水平长度为
1/2 + 1*cos30° + 1*cos60°
实际正方形边长为 2*(1/2 + 1*cos30° + 1*cos60°)
推广出去,对于正十六边形
在四分之一图中共有三条斜边
所以将 90° 角分为 4 份,每份 22.5°
实际边长为 2*(1/2 + 1*cos22.5° + 1*cos45° + 1*cos67.5°)
可以发现,从四边形开始,每增加四条边,斜边数量+1
故斜边数量可以通过 n/2-1 得到,每次增加 90/(n/2) °
程序 1
#include<bits/stdc++.h>
using namespace std;
const double PI=acos(-1.0);
const double epsilon=PI/180.0; //角度转弧度
void solve()
{
int n;
cin>>n;
double tri=90.0/(n/2),trid=0.0,ans=0;
for(int i=1;i<n/2;i++)
{
trid+=tri;
ans+=cos(trid*epsilon);
}
cout<<fixed<<setprecision(9)<<(ans+0.5)*2<<'
';
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin>>T;
while(T--)
solve();
return 0;
}
解题思路 2
由于本题给定的 n 是偶数
故正方形与正 2n 边形恰好可以有4条边重合
所以这个正 2n 边形的内接圆直径恰好为外接最小正方形的直径
以正十二边形为例
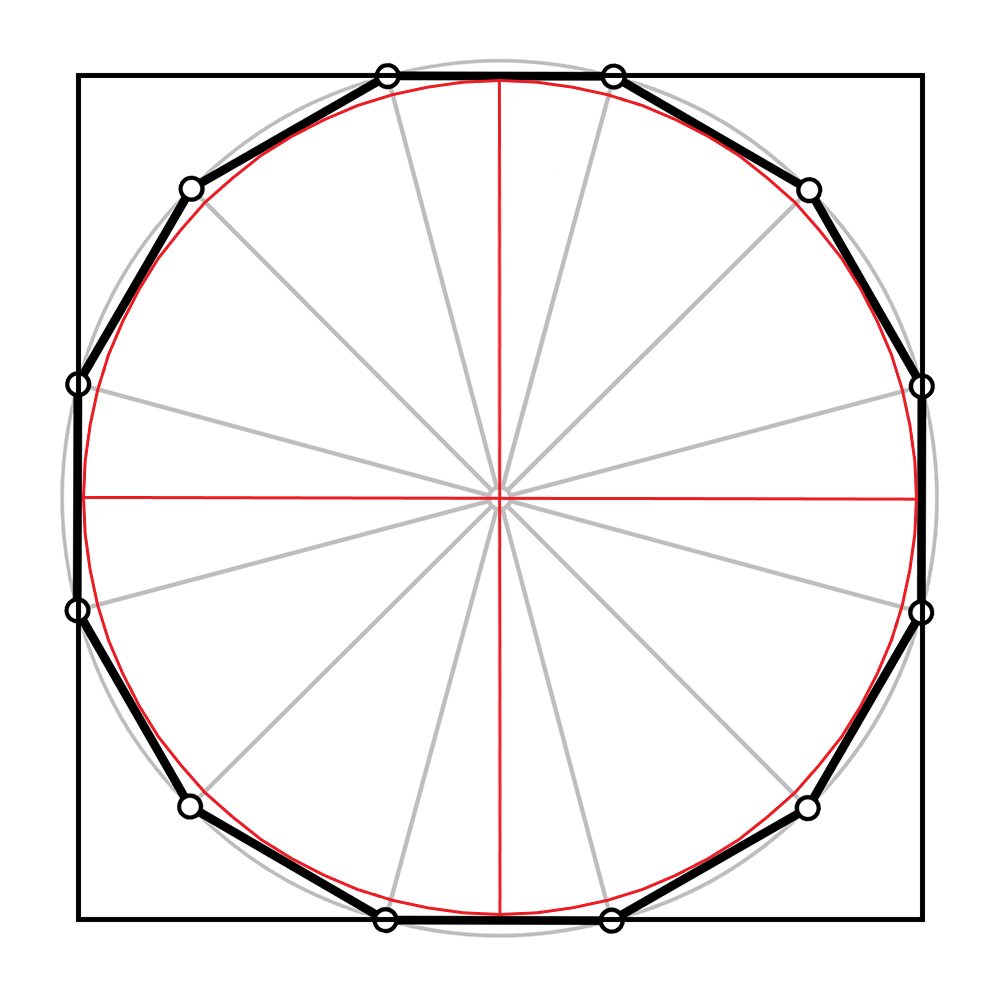
将正 2n 边形分成 2n 份,得到一个底边为 1 的等腰三角形
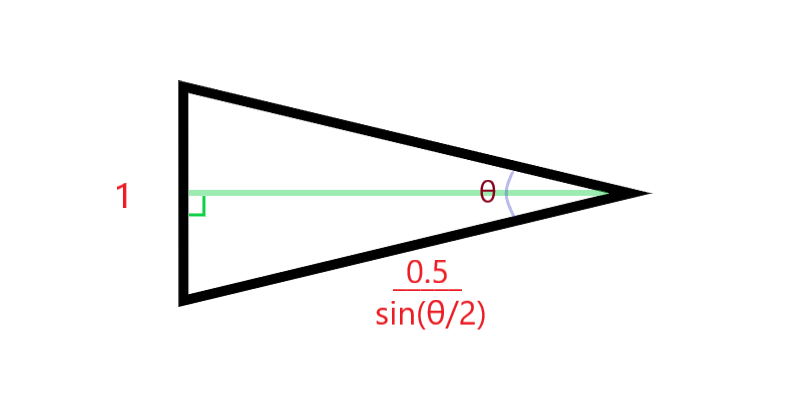
顶角 θ = 360/(2*n) = 180/n
计算可得 内接圆半径为 0.5/tan(θ/2)
所以答案即 1/tan(θ/2)
程序 2
#include<bits/stdc++.h>
using namespace std;
const double PI=acos(-1.0);
const double epsilon=PI/180.0; //角度转弧度
void solve()
{
int n;
cin>>n;
cout<<fixed<<setprecision(9)<<1.0/tan(90.0/n*epsilon)<<'
';
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin>>T;
while(T--)
solve();
return 0;
}