Codeforces 1336A/1337C

题面

题意

给定 n 个节点 n-1 条边组成的树，以节点 1 为根

现需要选出 k 个节点作为工业城市，其余城市均为旅游城市

问从所有工业城市出发走到根节点所经过的旅游城市数量之和的最大值

解题思路

反向思考，假定整个图全都是工业城市，那我们就需要选出 n-k 个旅游城市即可

既然以节点 1 为树根，那么对于每个节点，我们可以计算出以这个节点为根的子树中包含的节点数量以及这个节点拥有的祖先节点数量

可以发现，根据贪心，我们选择的旅游城市都是尽可能靠近根节点的

毫无疑问，第一步肯定是将根节点选成旅游城市，那么此时我们的答案就是 n-1，即此时工业城市的数量

以样例一的图为例

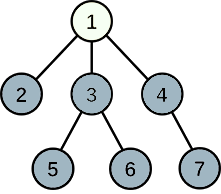
第一步选择 1 为旅游城市后，答案为 6 ，即工业城市数量

那么第二步——

　　如果我们选择 3 作为旅游城市，可以发现在节点 5 和节点 6 的路径上都增加了一个旅游城市，所以此时的答案为 6-1+2=7

　　如果我们选择 4 作为旅游城市，可以发现在节点 7 的路径上增加了一个旅游城市，所以此时的答案为 6-1+1=6

　　其余的，如果选择 2 5 6 7 作为旅游城市，则并不会有其余任意一个工业城市会经过这些旅游城市，答案会变成 6-1+0=5

综上，如果接下来选择某个节点 i 作为旅游城市，

那么对答案的“增加的贡献”就是以节点 i 为根的子树（不包括节点 i ）包含的节点数量

对答案的“减少的贡献”就是节点 i 的所有祖先节点中的旅游城市数量

又因为贪心可知，我们要么增加（增加的贡献），要么减少（减少的贡献），才能答案的值取到最大

且越靠近根节点的节点，子节点的数量又多，祖先节点的数量又少，肯定会优先取得

所以每个节点对答案的贡献就可以转化成 以节点 i 为根的子树（不包括节点 i ）包含的节点数量 - 节点 i 的祖先节点数量

处理出来后排序，再从大开始取 n-k 个即可

完整程序

设根节点 1 的深度为 0

那么每个节点的祖先节点数量也就成为了每个节点的深度

对于以节点 i 为根的子树（不包括节点 i ）包含的节点数量，dfs递归求和即可

(Pretests: 264ms/2000ms)

(System Tests: 327ms/2000ms)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

vector<int> G[200050];
bool vis[200050];

struct node
{
    int cnt,dis; //cnt存子树除该节点外的节点数量，dis存节点深度
    bool operator < (const node& a) const
    {
        return cnt-dis>a.cnt-a.dis; //按照对答案的贡献(cnt-dis)从大到小排序
    }
}ar[200050];

int dfs(int pos,int fa)
{
    vis[pos]=true; //标记访问
    ar[pos].dis=ar[fa].dis+1; //节点深度=父节点节点深度+1
    for(int it:G[pos])
        if(!vis[it])
            ar[pos].cnt+=dfs(it,pos); //求除自己以外子树中节点数量之和
    return ar[pos].cnt+1; //返回时要加上自己
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int n,k,a,b;
    cin>>n>>k;
    for(int i=1;i<n;i++)
    {
        cin>>a>>b;
        G[a].push_back(b);
        G[b].push_back(a);
    }
    ar[0].dis=-1; //特殊处理下，dis[1]=dis[0]+1=0 -> dis[0]=-1
    dfs(1,0);
    sort(ar+1,ar+n+1);
    ll ans=0;
    for(int i=1;i<=n-k;i++)
        ans+=ar[i].cnt-ar[i].dis;
    cout<<ans<<'
';

    return 0;
}