写在前面 - 本篇用到的输入和存图方法
输入方式:
第一行两个数 n 和 root ,表示树共有 n 个节点,其中以编号为 root 的作为根节点
接下来 n-1 行,每行两个整数 a b ,表示节点 a 与节点 b 相连
const int MAXN=1e4+50;
int dfs_order[MAXN];
int euler_order1[MAXN];
int euler_order2[MAXN];
bool vis[MAXN]; //访问标记
vector<int> G[MAXN]; //邻接表存图
int pos;
int n,root,a,b;
scanf("%d%d",&n,&root);
for(int i=1;i<n;i++)
{
scanf("%d%d",&a,&b);
G[a].push_back(b);
G[b].push_back(a);//双向存边
}
DFS序
顾名思义,DFS序就代表着树从根节点开始dfs的访问顺序
也可以当作访问每个节点的时间戳
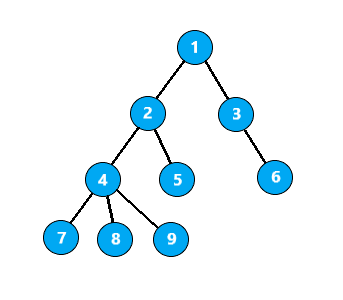
以这棵树为例,根节点为 1
按照从左到右的顺序搜索,则它的搜索顺序便是

在图中的顺序表示为
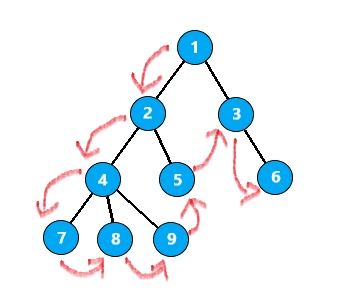
DFS序的搜索代码
void dfs(int p)
{
dfs_order[++pos]=p; //访问到节点p时,++pos作为访问到的时间
vis[p]=true;//标记访问
for(int i:G[p])//再搜索未访问过的与p相邻的节点
if(!vis[i])
dfs(i);
}
欧拉序
欧拉序长得跟dfs序相差无几
储存的则是从根节点开始,按照dfs的顺序经过所有点再绕回原点的路径
共存在两种欧拉序
欧拉序 1
这一种欧拉序相当于是在dfs的时候,如果储存节点的栈变化一次,就把栈顶的节点编号记录下来
也就是说,每当访问完一个节点的子树,则需要返回一次该节点,再继续搜索该节点的其余子树
在树上的移动过程为
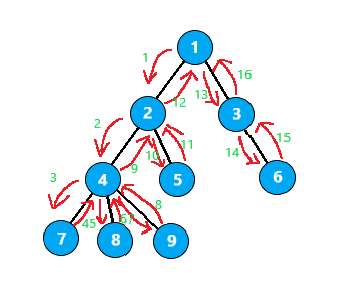
它的搜索顺序便是

欧拉序 1 的搜索代码
void euler_dfs1(int p)
{
euler_order1[++pos]=p;
vis[p]=true;
for(int i:G[p])
if(!vis[i])
{
euler_dfs1(i);
euler_order1[++pos]=p; //与dfs序的差别,在搜索完一棵子树后就折返一次自己
}
} //数组需要开2倍n大
欧拉序 2
这一种欧拉序相当于是在dfs的时候,如果某个节点入栈,就把这个节点记录下来,直到后面的操作中这个节点出栈,再记录一次这个节点
也就是说,每个节点严格会在记录中出现两次,第一次是搜索到它的时候,第二次是它的子树完全被搜索完的时候
除根节点外,每个节点严格两个入度两个出度
在树上的移动过程为
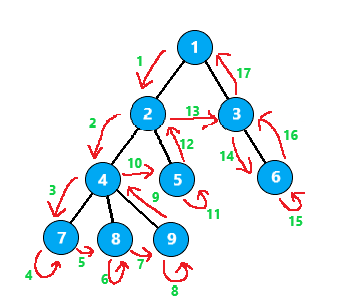
它的搜索顺序便是

可以发现,某个节点在顺序中出现的两次所围成的区间,就表示这个节点与它的子树
欧拉序 2 的搜索代码
void euler_dfs2(int p)
{
euler_order2[++pos]=p;
vis[p]=true;
for(int i:G[p])
if(!vis[i])
euler_dfs2(i);
euler_order2[++pos]=p; //与dfs序的差别,在所有子树搜索完后再折返自己
} //数组需要开2倍n大
样例输入 & 程序
Sample Input :
9 1
1 2
1 3
2 4
2 5
3 6
4 7
4 8
4 9
Sample Output :
DFS Order :
1 2 4 7 8 9 5 3 6
Euler Order 1 :
1 2 4 7 4 8 4 9 4 2 5 2 1 3 6 3 1
Euler Order 2 :
1 2 4 7 7 8 8 9 9 4 5 5 2 3 6 6 3 1
模板程序:
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e4+50;
int dfs_order[MAXN],euler_order1[MAXN*2],euler_order2[MAXN*2];
bool vis[MAXN];
vector<int> G[MAXN];
int pos;
void dfs(int p)
{
dfs_order[++pos]=p;
vis[p]=true;
for(int i:G[p])
if(!vis[i])
dfs(i);
}
void euler_dfs1(int p)
{
euler_order1[++pos]=p;
vis[p]=true;
for(int i:G[p])
if(!vis[i])
{
euler_dfs1(i);
euler_order1[++pos]=p;
}
}
void euler_dfs2(int p)
{
euler_order2[++pos]=p;
vis[p]=true;
for(int i:G[p])
if(!vis[i])
euler_dfs2(i);
euler_order2[++pos]=p;
}
int main()
{
int n,root,a,b;
scanf("%d%d",&n,&root);
for(int i=1;i<n;i++)
{
scanf("%d%d",&a,&b);
G[a].push_back(b);
G[b].push_back(a);
}
puts("DFS Order :");
memset(vis,false,n+5);
pos=0;
dfs(root);
for(int i=1;i<=pos;i++)
printf("%d ",dfs_order[i]);
putchar('
');
puts("Euler Order 1 :");
memset(vis,false,n+5);
pos=0;
euler_dfs1(root);
for(int i=1;i<=pos;i++)
printf("%d ",euler_order1[i]);
putchar('
');
puts("Euler Order 2 :");
memset(vis,false,n+5);
pos=0;
euler_dfs2(root);
for(int i=1;i<=pos;i++)
printf("%d ",euler_order2[i]);
putchar('
');
return 0;
}
应用 - 例题
1 - Codeforces 1006E

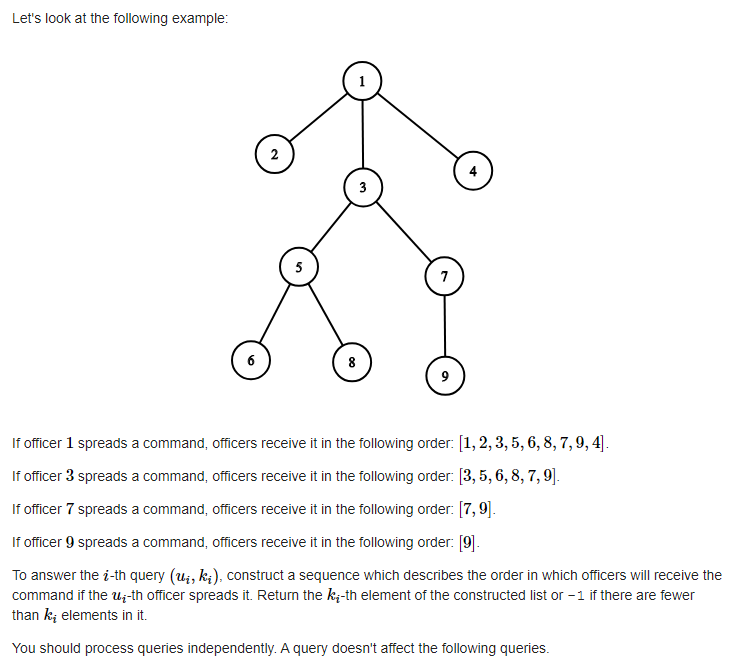

dfs序 的裸题
一棵 n 个节点的树,每条边都是单向边,第二行 n-1 个数分别对应 2,3,4... 节点的父节点编号
q 次询问,每次询问包含两个数 u k ,要求输出在dfs序中从 u 开始往后数到第 k 个所表示的节点,如果这个节点不存在于 u 的子树中,输出 -1
记录下处理dfs序时某个节点入栈时间 in 、出栈时间 out 以及dfs序实际表示的节点 即可
如果 in[u]+k-1 > out[u] 说明这个节点不包含于 u 的子树中
否则输出 dfs_order[in[u]+k-1]
#include<bits/stdc++.h>
using namespace std;
vector<int> G[200050];
int dfs_order[200050],in[200050],out[200050],pos;
void dfs(int p)
{
in[p]=++pos;
dfs_order[pos]=p;
for(int it:G[p])
dfs(it);
out[p]=pos;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int n,q,d,a,b;
cin>>n>>q;
for(int i=1;i<n;i++)
{
cin>>d;
G[d].push_back(i);
}
pos=0;
dfs(1);
while(q--)
{
cin>>a>>b;
if(in[a]+b-1>out[a])
cout<<"-1
";
else
cout<<dfs_order[in[a]+b-1]<<'
';
}
return 0;
}
2 - LibreOJ #144
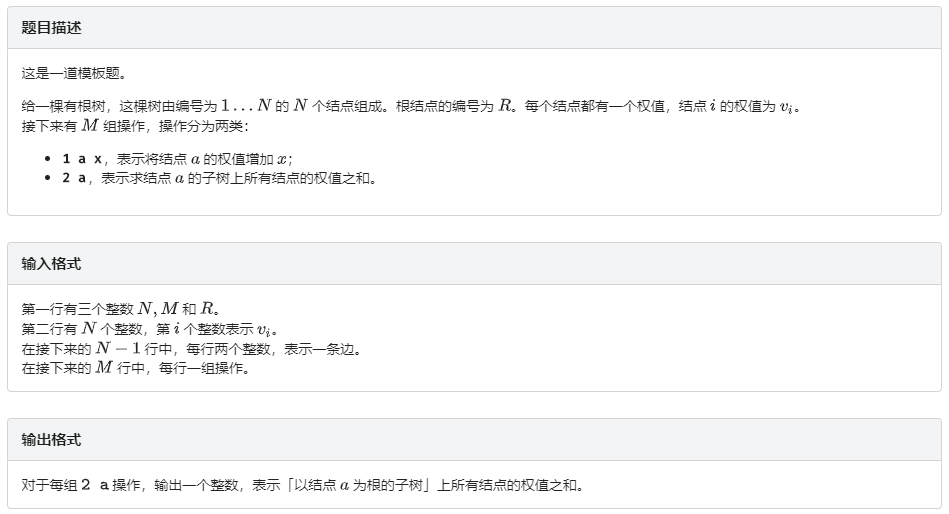
对树的权值进行 点修改 和 子树和查询
可以以 dfs序 的时间戳作为索引来维护一个树状数组
将每个节点入栈的时间 in 和出栈的时间 out 记录下来
则这个节点与它的子树就在区间 [ in , out ] 中
查询操作只要取 sum(out) - sum(in-1) 作为答案即可
修改操作只要修改入栈时间 in 那个点的值即可
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,ar[1000050],in[1000050],out[1000050],pos=0;
bool vis[1000050];
vector<int> G[1000050];
ll tree[1000050];
int lowbit(int x)
{
return x&(-x);
}
void add(int p,ll d)
{
while(p<=n)
{
tree[p]+=d;
p+=lowbit(p);
}
}
ll sum(int p)
{
ll r=0;
while(p>0)
{
r+=tree[p];
p-=lowbit(p);
}
return r;
}
void dfs(int p)
{
in[p]=++pos; //入栈时间
vis[p]=true;
for(int it:G[p])
if(!vis[it])
dfs(it);
out[p]=pos; //出栈时间
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int m,r,a,b,kd;
cin>>n>>m>>r;
for(int i=1;i<=n;i++)
cin>>ar[i];
for(int i=1;i<n;i++)
{
cin>>a>>b;
G[a].push_back(b);
G[b].push_back(a);
}
dfs(r);
for(int i=1;i<=n;i++)
add(in[i],ar[i]); //以时间作为索引建立树状数组
while(m--)
{
cin>>kd;
if(kd==1)
{
cin>>a>>b;
add(in[a],b);
}
else
{
cin>>a;
cout<<sum(out[a])-sum(in[a]-1)<<'
';
}
}
return 0;
}
3 - LibreOJ #145
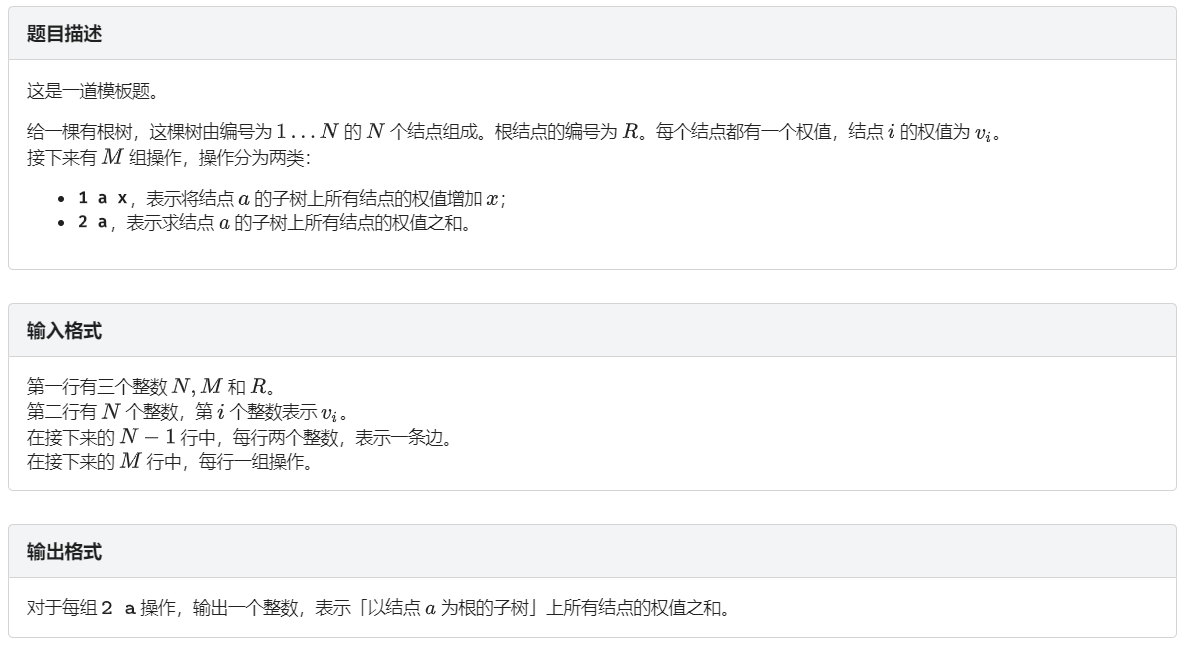
对树的权值进行 全子树修改 和 子树和查询
与上一题相差无几
可以以 dfs序 的时间戳作为索引来维护一棵线段树
依然按照入栈时间 in 和出栈时间 out 作为索引
然后套上区间修改和区间求和的线段树即可
又因为线段树的某个节点维护的是一段区间,也就是一段时间
所以在建树的时候要注意,再引入一个 anti_in 数组记录与 in 数组相反的数据
具体用法如下
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=1e6+50;
int n,ar[MAXN];
bool vis[MAXN];
vector<int> G[MAXN];
int in[MAXN],out[MAXN],pos=0,anti_in[MAXN];
struct node
{
ll l,r,sum,lazy;
}tree[MAXN*4];
void push_up(int id)
{
tree[id].sum=tree[id<<1].sum+tree[id<<1|1].sum;
}
void push_down(int id)
{
if(tree[id].lazy)
{
int m=tree[id].r-tree[id].l+1;
tree[id<<1].lazy+=tree[id].lazy;
tree[id<<1|1].lazy+=tree[id].lazy;
tree[id<<1].sum+=tree[id].lazy*(m-(m>>1));
tree[id<<1|1].sum+=tree[id].lazy*(m>>1);
tree[id].lazy=0;
}
}
void buildTree(int id,int l,int r)
{
tree[id].l=l;
tree[id].r=r;
tree[id].lazy=0;
if(l==r)
{
tree[id].sum=ar[anti_in[l]]; //这里引用的是第l(或r)的时间访问到的节点id传给ar数组获取原有的权值
return;
}
ll mid=(l+r)>>1;
buildTree(id<<1,l,mid);
buildTree(id<<1|1,mid+1,r);
push_up(id);
}
void update(int id,int L,int R,ll val)
{
if(L<=tree[id].l&&R>=tree[id].r)
{
tree[id].sum+=val*(tree[id].r-tree[id].l+1);
tree[id].lazy+=val;
return;
}
push_down(id);
int mid=(tree[id].r+tree[id].l)>>1;
if(L<=mid)
update(id<<1,L,R,val);
if(R>mid)
update(id<<1|1,L,R,val);
push_up(id);
}
ll query_sum(int id,int L,int R)
{
if(L<=tree[id].l&&R>=tree[id].r)
return tree[id].sum;
push_down(id);
int mid=(tree[id].r+tree[id].l)>>1;
ll ans=0;
if(L<=mid)
ans+=query_sum(id<<1,L,R);
if(R>mid)
ans+=query_sum(id<<1|1,L,R);
return ans;
}
void dfs(int p)
{
in[p]=++pos; //in记录节点p入栈的时间
anti_in[pos]=p; //anti_in记录在某个时间访问到的节点的id
vis[p]=true;
for(int it:G[p])
if(!vis[it])
dfs(it);
out[p]=pos;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int m,r,a,b,kd;
cin>>n>>m>>r;
for(int i=1;i<=n;i++)
cin>>ar[i];
for(int i=1;i<n;i++)
{
cin>>a>>b;
G[a].push_back(b);
G[b].push_back(a);
}
dfs(r);
buildTree(1,1,n); //建立线段树
while(m--)
{
cin>>kd;
if(kd==1)
{
cin>>a>>b;
update(1,in[a],out[a],b);
}
else
{
cin>>a;
cout<<query_sum(1,in[a],out[a])<<'
';
}
}
return 0;
}