【数据结构】ST算法

区间最值查询问题的一般解法

区间最值查询问题，即RMQ（Range Minimum/Maximum Query）

常见解法有朴素算法——O(n)预处理、O(n)查询，总体复杂度O(n+nq)

线段树——O(nlogn)预处理、O(logn)查询，总体复杂度O((n+q)logn)

ST算法——O(nlogn)预处理、O(1)查询，总体复杂度O(nlogn+q)

ST算法

ST算法是基于倍增算法与动态规划的一个解决静态区间RMQ的算法

忽略朴素算法，与线段树进行对比

优点是查询的时间复杂度为线性，对于查询多的题型有利

缺点是只支持对静态区间的查询（初始化后就不能修改值），且空间复杂度在大部分情况下比线段树要大（线段树保守情况为O(4n)，ST算法为O(nlogn)）

ST算法的实现

预处理部分

①：基于倍增算法，我们需要预处理从某个位置 i 开始往后 2 的次方倍长度区间内的最值并储存起来

②：假设此次查询的区间内共有 x 个元素，则需要返回 logx 向下取整，为保证算法O(1)实现，所以这一步也进行预处理储存

查询部分

虽然运用了倍增算法

很容易想到可以从查询的左边界 L 开始

每次将 log(R-L+1)向下取整 个长度的区间的最值取出来与答案进行取大（这里的最值就是预处理部分的①）

再更新左边界 L 继续取下去

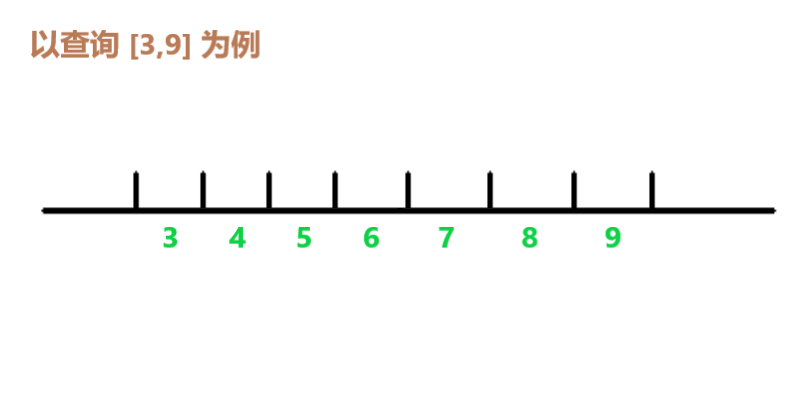
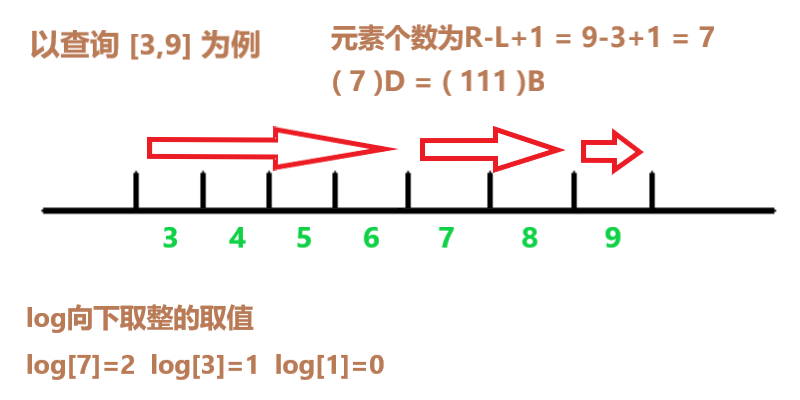
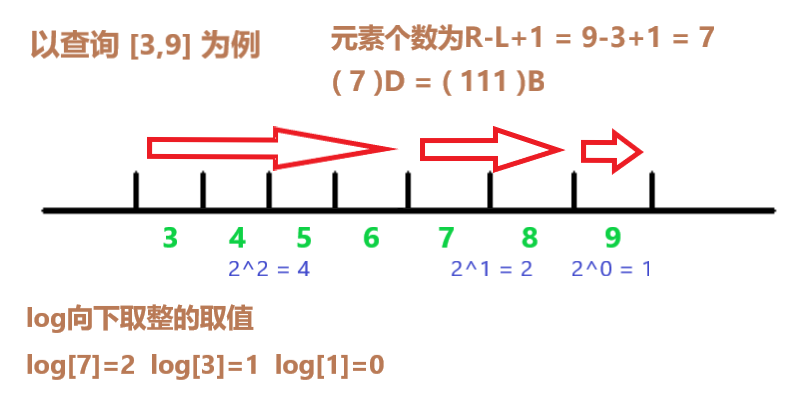
（图示箭头即为每次L的更新过程）

也可以看成将R-L+1转成二进制后，根据1的位置来处理接下来要走多少步

但是这种做法显然是O(logn)级别的

实际上，既然已经预处理出来从某个位置 i 开始往后的 2 从次方倍长度区间中的最值

那我们就可以根据 log(R-L+1) 的值

从 L 开始往右取 2^log 长度区间内的最值

再从 R 开始往左取 2^log 长度区间内的最值

将这两个最值取大即为答案，时间复杂度为O(1)

可以保证的是，L 往右取的区间与R往左取的区间一定有重叠部分，且不会超过对方的位置

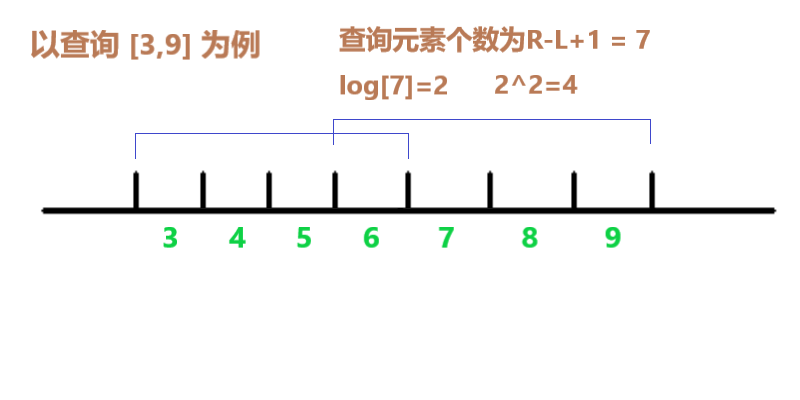
（图中两线段即代表取的区间）

ST算法的代码实现

代码中以求最大值为例，改为最小值只需要把max改成min即可

数据储存方式

const int MAXN=100050,MAXF=18;
int ar[MAXN];//原数组
int dp[MAXN][MAXF];//dp[i][j]表示从i开始往右2^j长度的区间内的最值
int LOG[MAXN];//LOG[i]=log2(i)向下取整

保证 2^MAXF-1>MAXN，防止越界

预处理部分

对于dp数组

可以发现2⁰=1，所以 dp[i][0] = ar[i] ，将第0层处理掉（如无其他条件，可以忽略ar数组直接读入dp数组）

从j=1开始，与其他问题的倍增算法类似，根据dp思想，由 2ⁱ = 2^i-1 + 2^i-1 可以得到状态转移方程为

dp[i][j] = max( dp[i][j-1] , dp[i+(1<<(j-1))][j-1] )

用语言描述就是

从 i 位置开始 2^j 长度区间内的最大值，可以由 “从 i 位置开始 2^j-1 长度区间内的最大值” ，“从 i+2^j-1 位置开始 2^j-1 长度区间内的最大值” 这两个值取大转移而来

for(int i=1;i<=n;i++)
    dp[i][0]=ar[i];
for(int j=1;(1<<j)<=n;j++)//如果长度已经超过n，则没有继续处理的必要
    for(int i=1;i+(1<<(j-1))<=n;i++)//如果从i开始往右没法取2^j长度的区间，则无法继续处理
        dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);

对于LOG数组

根据除法整除的性质，log数组可以通过

log[i] = log[i/2] + 1

转移而来 （ log[1] = 0 ）

LOG[1]=0;
for(int i=2;i<=n;i++)
    LOG[i]=LOG[i/2]+1;

查询部分

输入查询区间 L 与 R

首先得到区间内元素个数为 R-L+1 ，对应的两端区间长度为 2^LOG[R-L+1]

令d=LOG[R-L+1]

可以得到从L开始往右这段区间以 L 为左边界，则最大值为 dp[L][d]

从R开始往左取的这段区间左边界为 R-2^d+1，则最大值为 dp[R-(1<<d)+1][d]

两个值取大输出即为答案

scanf("%d%d",&L,&R);
d=LOG[R-L+1];
printf("%d
",max(dp[L][d],dp[R-(1<<d)+1][d]));

完整程序（模板）

模板例题：Luogu P3865

（这题如果出现TLE，尝试使用快读，题目已说明）

#include<bits/stdc++.h>
using namespace std;

const int MAXN=100050,MAXF=18;
int ar[MAXN];
int dp[MAXN][MAXF];
int LOG[MAXN];

int main()
{
    int n,q,L,R,d;
    scanf("%d%d",&n,&q);
    
    LOG[1]=0;
    for(int i=2;i<=n;i++)
        LOG[i]=LOG[i/2]+1;
    
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&ar[i]);
        dp[i][0]=ar[i];
    }

    for(int j=1;(1<<j)<=n;j++)
        for(int i=1;i+(1<<(j-1))<=n;i++)
            dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);

    while(q--)
    {
        scanf("%d%d",&L,&R);
        d=LOG[R-L+1];
        printf("%d
",max(dp[L][d],dp[R-(1<<d)+1][d]));
    }

    return 0;
}

参考了forever_dreams的CSDN博客81127189