E. Are You Fired?（思维）

题：https://codeforces.com/contest/1358/problem/E

题意：给定一个n个数的数组，问是否存在k，使得任意连续的k个数之和都大于零，若存在就输出k，否则输出-1。特别地，题目保证数组后floor(n/2)个数的值均为 x。

分析： 贪心地去考虑的化，k的大小一定大于floor（n/2），因为若x<=0的话，一定要多“拉”几个数来凑成总和大于0，若x>0的话，k<=floor(n/2)的情况对于后面的数来说一定成立，还不如多扩大空间让不满足条件的满足。

　　　其次，我们发现实际上只要枚举后缀和即可，如图所示枚举到3个后缀的情况（其中黑线是转移过程，具体在代码中表现为减去x）

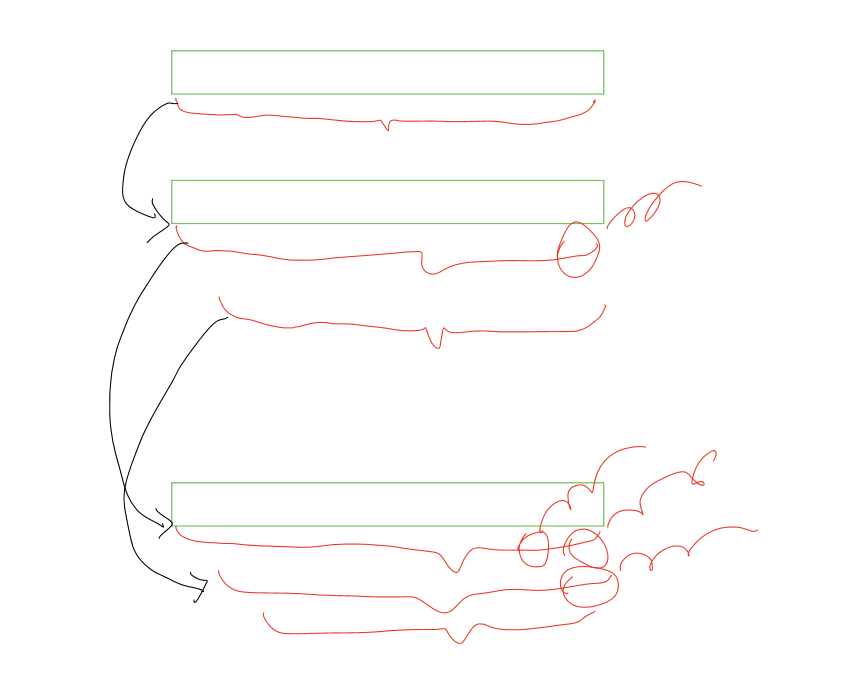
　　　从中，我们不难发现，只要我们枚举的这些后缀（伴随枚举更新）中的最小值大于0即是合法方案，所以我们只要记录枚举过的后缀的最小值即可。

#include<bits/stdc++.h>
#define lowbit(i) i&(-i)
using  namespace std;
typedef long long ll;
const int M=1e6+6;
const ll INF=1e18;
int n;
ll k;
ll a[M],sum[M];
ll solve(int x){
    return sum[k]-sum[x-1];
}
int main(){

    scanf("%d",&n);
    k=(n+1)/2;
    for(int i=1;i<=k;i++){
        scanf("%lld",&a[i]);
        sum[i]=sum[i-1]+a[i];
    }
    int x;
    scanf("%d",&x);
    ll minn=INF;
    ll ans=-1;
    ll half=1ll*n/2;
    for(int i=1;i<=k;i++){
        ll tmp=solve(i)+half*x;
        if(minn==INF)
            minn=tmp;
        else{
            minn-=x;///后缀的转移，因为只要最小值进行转移即可，不必对所有后缀进行转移
            minn=min(minn,tmp);
        }
            
        if(minn>0)
            ans=n-i+1;
    }
    printf("%lld
",ans);
    return 0;
}