poj2243 给出m个模式串，求长度小于n的且存在模式串的字符串数有多少个（a~z）（思维构造+ac自动机）

题：http://acm.hdu.edu.cn/showproblem.php?pid=2243

题意：给出m个模式串，求长度小于n的且存在模式串的字符串数有多少个（a~z）

分析：我们反着来，用总的减去不包含的，总的很容易想到，每个位置都有26个选择，所以是Σ¹_n26ⁱ  不包含的 这里  有解决恰好长度为n的方法，但这里要小于等于n的全部；

　　　其实解决方法类似，将上述的解题方法中的方案矩阵设为A，那么我们构造如下矩阵（含解释）

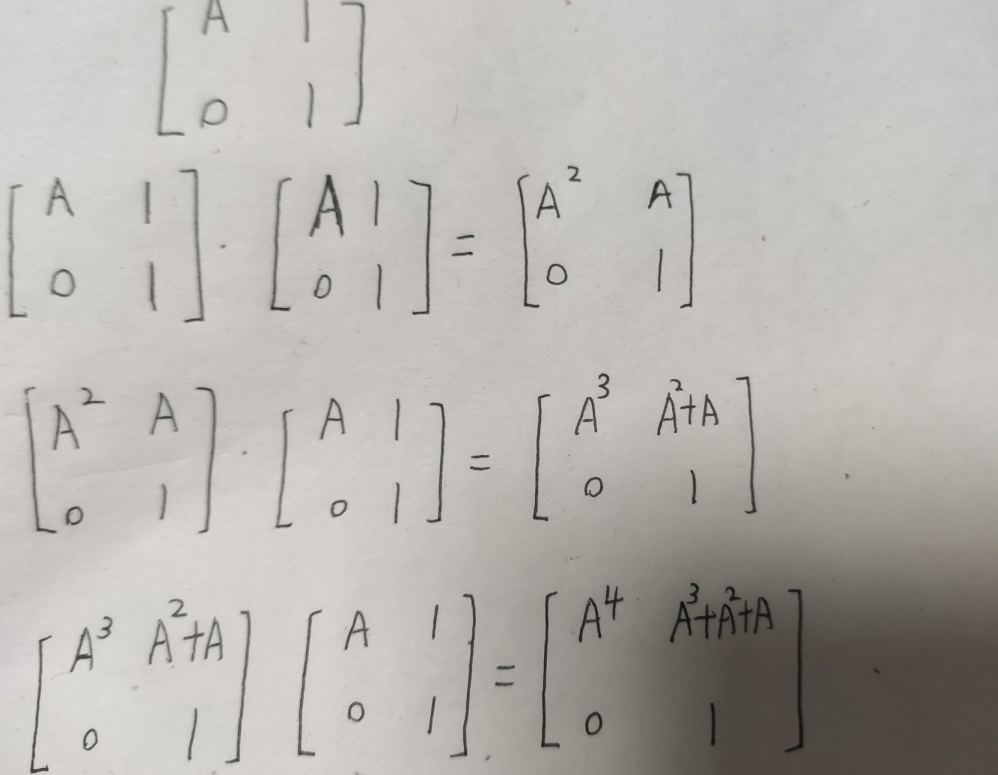
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<queue>
#include<cmath>
using namespace std;
typedef unsigned long long ll;
const int N=1e3+3;
const int maxn=26;
struct ac{
    int trie[N][maxn],fail[N];
    ll A[N][N],T[N][N],tmp[N][N];
    bool end[N];
    int root,tot;
    int newnode(){
        for(int i=0;i<maxn;i++)
            trie[tot][i]=-1;
        end[tot++]=0;
        return tot-1;
    }
    void init(){
        memset(A,0,sizeof(A));
        memset(end,false,sizeof(end));
        tot=0;
        root=newnode();
    }
    void insert(char buf[]){
        int now=root,len=strlen(buf);
        for(int i=0;i<len;i++){
            if(trie[now][buf[i]-'a']==-1)
                trie[now][buf[i]-'a']=newnode();
            now=trie[now][buf[i]-'a'];
        }
        end[now]=true;
    }
    void getfail(){
        queue<int>que;
        while(!que.empty())
            que.pop();
        fail[root]=root;
        for(int i=0;i<maxn;i++){
            if(trie[root][i]==-1)
                trie[root][i]=root;
            else{
                fail[trie[root][i]]=root;
                que.push(trie[root][i]);
            }
        }
        while(!que.empty()){
            int now=que.front();
            que.pop();
            if(end[fail[now]])
                end[now]=true;
            for(int i=0;i<maxn;i++){
                if(trie[now][i]!=-1){
                    fail[trie[now][i]]=trie[fail[now]][i];
                    que.push(trie[now][i]);
                }
                else
                    trie[now][i]=trie[fail[now]][i];
            }
        }
    }
    void getA(){
        for(int i=0;i<tot;i++)
            for(int j=0;j<maxn;j++)
                if(!end[i]&&!end[trie[i][j]]){
                    A[i][trie[i][j]]++;
                }
                    
        ///构造所说的前缀和的矩阵
        for(int i=0;i<=tot;i++)
            A[i][tot]=1; 
    }
    void mul(ll a[][N],ll b[][N],int len){
        for(int i=0;i<len;i++)
            for(int j=0;j<len;j++){
                tmp[i][j]=0;
                for(int k=0;k<len;k++)
                    tmp[i][j]=(tmp[i][j]+a[i][k]*b[k][j]);
            }
        for(int i=0;i<len;i++)
            for(int j=0;j<len;j++)
                a[i][j]=tmp[i][j];
    }
    void solve(ll n,ll len){///这里的俩个参量要是换成int会t。。。。 
        memset(T,0,sizeof(T));
        for(int i=0;i<len;i++)
            T[i][i]=1;
        while(n){
            if(n&1)
                mul(T,A,len);
            mul(A,A,len);
            n>>=1;
        }
        
    }
}AC;
char s[10];
int main(){
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF){
        AC.init();
        for(int i=1;i<=n;i++){
            scanf("%s",s);
            AC.insert(s);
        }
        AC.getfail();
    //    cout<<AC.tot<<"!!"<<endl;
        AC.getA();
        AC.solve(m,AC.tot+1);///不包含的 
        
            
        ll ans=0;
        for(int i=0;i<=AC.tot;i++)
            ans=(ans+AC.T[0][i]);
        ///全部的 
        AC.A[0][0]=26,AC.A[0][1]=1;
        AC.A[1][0]=0, AC.A[1][1]=1;
        AC.solve(m+1,2);
        ///全部-不包含的 
        printf("%I64u
",AC.T[0][1]-ans);
    }
    return 0;
}