Matrix Inversion: Finding the Inverse of a Matrix

Matrix Inversion:

  Finding the Inverse of a Matrix

For matrices, there is no such thing as division. You can add, subtract, and multiply matrices, but you cannot divide them. There is a related concept, though, which is called "inversion". First I'll discuss why inversion is useful, and then I'll show you how to do it.

---

Think back to when you first learned about how to solve linear equations. If you were given something like "3x = 6", you would solve by dividing both sides by 3. Since multiplying by1/3 is the same as dividing by 3, you could also multiply both sides by 1/3 to get the same answer: x = 2. If you needed to solve something like "(3/2)x = 6", you could still divide both sides by 3/2, but it was probably easier to multiply both side by 2/3. The reciprocal fraction 2/3 is the inverse of 3/2 because, if you multiply the two fractions, you get 1, which is, in this context, called "the (multiplicative) identity": 1 is called the identity because multiplying something by 1 doesn't change its value.

This terminology and these facts are very important for matrices. If you are given a matrix equation likeAX = C, where you are given A and C and are told to figure out X, you would like to "divide off" the matrix A. But you can't do division with matrices. On the other hand, what if you could find the inverse ofA, something similar to finding the reciprocal fraction above? The inverse of A, written as "A^–1" and pronounced "A inverse", would allow you to cancel off the A from the matrix equation and then solve forX.

AX = C 
A^–1AX = A^–1C 
IX = A^–1C 
X = A^–1C

How did "A^–1AX" on the left-hand side of the equation turn into "X"? Think back to the nature of inverses for regular numbers. If you have a number (such as 3/2) and its inverse (in this case, 2/3) and you multiply them, you get 1. And 1 is the identity, so called because 1x = x for any number x. It works the same way for matrices. If you multiply a matrix (such as A) and its inverse (in this case, 
A^–1), you get the identity matrix I. And the point of the identity matrix is that IX = X for any matrix X(meaning "any matrix of the correct size", of course).

It should be noted that the order in the multiplication above is important and is not at all arbitrary. Recall that, for matrices, multiplication is not commutative. That is, AB is almost never equal to BA. So multiplying the matrix equation "on the left" (to get A^–1AX) is not at all the same thing as multiplying "on the right" (to get AXA^–1). And you can not say that the product AXA^–1 equals A^–1AX, because you can't switch around the order in the multiplication. Instead, you have to multiply A^–1 on the left, putting it right next to the A in the original matrix equation. And since you have to do the same thing to both sides of an equation when you're solving, you must multiply "on the left" on the right-hand side of the equation as well, resulting in A^–1C. You cannot be casual with your placement of the matrices; you must be precise, correct, and consistent. This is the only way to successfully cancel off A and solve the matrix equation.

---

As you have seen above, inverse matrices can be very useful for solving matrix equations. But, given a matrix, how do you invert it? How do you find the inverse? The technique for inverting matrices is kind of clever. For a given matrix A and its inverse A^–1, we know we have A^–1A = I. We're going to use the identity matrix I in the process for inverting a matrix.

• Find the inverse of the following matrix.

First, I write down the entries the matrix A, but I write them in a double-wide matrix:

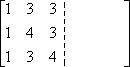
In the other half of the double-wide, I write the identity matrix:

Now I'll do matrix row operations to convert the left-hand side of the double-wide into the identity. (As always with row operations, there is no one "right" way to do this. What follows are just the steps that happened to occur to me. Your calculations could easily look quite different.)

Now that the left-hand side of the double-wide contains the identity, the right-hand side contains the inverse. That is, the inverse matrix is the following:

Note that we can confirm that this matrix is the inverse of A by multiplying the two matrices and confirming that we get the identity:   Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved

Warning: Not all matrices can be inverted. Recall that the inverse of a regular number is its reciprocal, so 4/3 is the inverse of 3/4, 2 is the inverse of 1/2, and so forth. But there is no inverse for 0, because you cannot flip 0/1 to get 1/0 (since division by zero doesn't work). For similar reasons (which you may or may not encounter in later studies), some matrices cannot be inverted.

---

Given a matrix A, the inverse A^–1 (if said inverse matrix in fact exists) can be multiplied on either side ofA to get the identity. That is, AA^–1 = A^–1A = I. Keeping in mind the rules for matrix multiplication, this says that A must have the same number of rows and columns; that is, A must be square. (Otherwise, the multiplication wouldn't work.) If the matrix isn't square, it cannot have a (properly two-sides) inverse. However, while all invertible matrices are square, not all square matrices are invertible.

Always be careful of the order in which you multiply matrices. For instance, if you are given B and Cand asked to solve the matrix equation AB = C for A, you would need to cancel off B. To do this, you would have to multiply B^–1 on B; that is, you would have to multiply on the right:

AB = C 
ABB^–1 = CB^–1 
AI = CB^–1 
A = CB^–1

The side on which you multiply will depend upon the exercise. Take the time to get this right.

---

There is only one "word problem" sort of exercise that I can think of that uses matrices and their inverses, and it involves coding and decoding.

• You receive a coded message. You know that each letter of the original message was replaced with a one- or two-digit number corresponding to its placement in the English alphabet, so "E" is represented by "5" and "W" by "23"; spaces in the message are indicated by zeroes. You also know that the message was transformed (encoded) by multiplying the message on the left by the following matrix:

Translate the coded message:

To do the decoding, I have to undo the matrix multiplication. To undo the multiplication, I need to multiply by the inverse of the encoding matrix. So my first step is to invert the coding matrix:

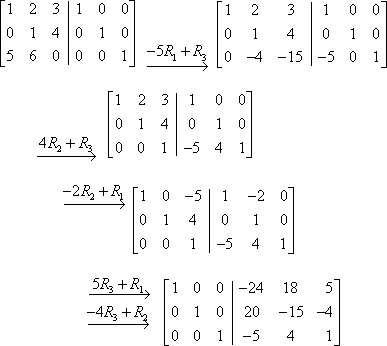
So the inverse matrix is:

My correspondent converted letters to numbers, and then entered those numbers into a matrixC. He then multiplied by this matrix by the encoding matrix A, and sent me the message matrixM. Since the encoding was done by multiplying C on the left, then I know the encoding equation was:

AC = M

To reverse the encoding, I need to multiply by A^–1 on the left:

A^–1AC = A^–1M 
C = A^–1M

This gives me:

At this point, the solution is a simple matter of doing the number-to-letter correspondence:

A	B	C	D	E	F	G	H	I	J	K	L	M
1	2	3	4	5	6	7	8	9	10	11	12	13

  Copyright © Elizabeth Stapel 1999-2009 All Rights Reserved

N	O	P	Q	R	S	T	U	V	W	X	Y	Z
14	15	16	17	18	19	20	21	22	23	24	25	26

T H E  L A W  I S  A N  A ...

(You can complete the decoding to view the original quotation.)

A better "code" could be constructed by shifting the letters first, adding some value to each letter's coded result, using a larger invertible matrix, etc, etc. The above example is fairly simplistic, and is intended only to show you the general methodology.

Be advised that, in "real life", the inverse is rarely a matrix filled with nice neat whole numbers like this. With any luck, though, especially if you're doing inverses by hand, you'll be given nice ones like this to do.